Overview
Valve Hammer Editor is a pretty common tool for making buildings and structures for games these days, and in some cases entire levels. It exports .MAP files containing solids, called “brushes”, which make up the solid areas of the building/structure/map. There are a few tools that can convert these to .BSP files for use in Quake, Quake II, etc., or into other formats, such as those used by Starsiege: Tribes.
This series of tutorials will explain how to load .MAP files, create accurate triangle representations of the solids (many people believe that .MAP files contain triangles—they are wrong), build an efficient BSP representing the data, generate and use portals/PVS’s, generate UV coordinates, generate a BVH for collision detection, and even explain a simple physics implementation that will allow you to have some fun with the .MAP files you loaded with your own engine.
I will present stable, fast, and robust routines, including the use of explicit stacking while building the BSP tree to avoid stack overflow on huge levels. In some cases I will use things to improve my own speed which most people might not have available to them, such as stack allocators. In these cases I will also explain how it can easily be done in an alternative way, although at the cost of speed.
By the end of the series you will be able to load any .MAP file from Valve Hammer Editor into your own engine and have fun rolling balls around the map or even taking the next small step up and putting a walking character into it.
Prerequisites
Our first goal is simply to get a graphical representation of the solids inside the file. You should start off by understanding the .MAP format. Here is a sample line from a solid in a .MAP file.
( 130 247 48 ) ( 257 247 48 ) ( 257 247 61 ) 143 [ 1 0 0 -18.2162 ] [ 0 0 -1 0.833384 ] 0 0.246667 0.24
The most important thing to note is that those 3 sets of points are not vertices. They are a plane described by 3 points, and those 3 points coincidentally are vertices on the actual solid, but don’t really have to be. The plane described by those 3 points is the plane for a single face of the solid. A face is just one side of the solid, so a cube has 6 faces, and would have 6 entries for that solid in the .MAP file. So if you try to read this data is just triangle data, you would basically end up with a cube with each face missing one triangle. For the time being, let’s ignore all of the rest of the data. Our only objective for this tutorial is to get the triangles that correctly create a graphical representation of the solids.
I will not cover how to load and parse the data out of the .MAP file. It’s text and you can do it any way you like. Flex/Bison is recommended, or just roll your own parser.
Let’s Get Started
So you have a parser and you know that those aren’t triangles in the .MAP file, they are planes pretending to be triangles. Now you need some utility functions. For the sake of accuracy, I strongly recommend using doubles rather than floats. I have vector, plane, ray, line-segment, etc. templates that allow me to specify whatever type I want, and I strongly suggest you do the same. The data will end up as 32-bit floating-point values, but while we are doing plane math, polygon splitting, etc., it will be to your advantage to have them all being 64-bit precision.
I am also not going to provide code for all of the base types you will need, but I will for some that are important. A vector class is a vector class is a vector class. They all have a Dot() and a Cross(). In my code, the * operator on a vector is the Dot() function, and % is Cross(). A line segment is just 2 vectors, p and q. p is the starting point and q is the end point. A ray is just a point and a normal. A plane is just a normal and a distance in that direction. But it has some important features that make it worth posting. Specifically, we need a way to convert from 3 points to a plane in standard form.
template <typename _tType, typename _tVec3Type>
class CPlane3Base {
// All is public. This class has no secrets.
public :
// == Various constructors.
LSE_INLINE LSE_CALLCTOR CPlane3Base() {
}
LSE_INLINE LSE_CALLCTOR CPlane3Base( const CPlane3Base<_tType, _tVec3Type> &_pPlane ) {
(*this) = _pPlane;
}
LSE_INLINE LSE_CALLCTOR CPlane3Base( const _tVec3Type &_vPoint0, const _tVec3Type &_vPoint1, const _tVec3Type &_vPoint2 ) {
n = (_vPoint1 - _vPoint0) % (_vPoint2 - _vPoint0);
n.Normalize();
dist = n.Dot( _vPoint0 );
}
// == Members.
/**
* Plane normal.
*/
_tVec3Type n;
/**
* Plane distance, signed.
*/
_tType dist;
};
…
typedef CPlane3Base<LSDOUBLE, CVector3High> CPlane3High;
Now we have a way to convert the 3 points in the .MAP file to a plane. Going back to the cube example, when you have done this for all 6 faces, you will have 6 planes that represent the solid region of the cube. This is called an H-representation, where H stands for “half space”, which is what planes usually are. They divide space in half, one side being good and the other side evil, or solid. Note that in .MAP files, the normal points towards the inside of the solid, and I have opted to reverse it so it points outwards. The following plane negation operator was used.
/**
* Negation operaor.
*
* \return Returns the negated form of this plane.
*/
CPlane3Base<_tType, _tVec3Type> LSE_CALL
operator - () const {
return CPlane3Base<_tType, _tVec3Type>( -n, -dist );
}
So How do We Get Triangle Data Out of a Bunch of Planes?
Let’s consider the case of a cube. The follow image shows the top plane of the cube, shown in blue. The bottom side is not represented at all because it does not intersect the blue plane, which represents the top of the cube. The plane for the top side is shown in blue, but the part that has been “sectioned off” by the side planes is shown in red.
We want to determine the line segments that surround the red part. By connecting those line segments we create a closed convex polygon, and once we have a polygon it will be possible to then create triangles.
There are 2 helper functions we will need. One gets a ray that represents the intersection of 2 planes, and 1 gets the point that represents the intersection of 3 planes. Again, templates are recommended so that you can use 64-bit doubles for your toolchains and 32-bit floats for your game engine.
/**
* Gets the intersection point of 3 planes if there is one. If not, false is returned.
*
* \param _pP0 Plane 1.
* \param _pP1 Plane 2.
* \param _pP2 Plane 3.
* \param _vRet The returned intersection point, valid only if true is returned.
* \return Returns true if the 3 planes intersect at a single point.
*/
template <typename _tType, typename _tPlaneType, typename _tVecType>
static LSE_INLINE LSBOOL LSE_CALL CIntersect::ThreePlanes( const _tPlaneType &_pP0, const _tPlaneType &_pP1, const _tPlaneType &_pP2, _tVecType &_vRet ) {
_tVecType vU = _pP1.n % _pP2.n;
_tType fDenom = _pP0.n * vU;
if ( CMathLib::AbsT( fDenom ) <= static_cast<_tType>(LSM_REAL_EPSILON) ) { return false; }
_vRet = (vU * _pP0.dist + _pP0.n.Cross( _pP1.n * _pP2.dist - _pP2.n * _pP1.dist )) / fDenom;
return true;
}
/**
* If the given planes intersect, the ray defining the intersection is returned. Planes must be normalized.
*
* \param _pP0 Plane 1.
* \param _pP1 Plane 2.
* \param _rRay The return ray.
* \return Returns true if the 2 planes intersect.
*/
template <typename _tType, typename _tPlaneType, typename _tRayType>
static LSE_INLINE LSBOOL LSE_CALL CIntersect::TwoPlanes( const _tPlaneType &_pP0, const _tPlaneType &_pP1, _tRayType &_rRay ) {
// Direction of the intersection.
_rRay.dir = _pP0.n % _pP1.n;
// If it is (near) 0, the planes are parallel (and separated) or coincident and not considered
// intersecting.
if ( _rRay.dir.Dot( _rRay.dir ) < static_cast<_tType>(LSM_REAL_EPSILON) ) { return false; }
// Finish the ray by computing a point on the intersection line.
_rRay.p = ((_pP1.n * _pP0.dist) - (_pP0.n * _pP1.dist)) % _rRay.dir;
return true;
}
Remember, rays are a point and a direction, both vector types, and the % operator is cross-product while the * operator is dot-product..
With these 2 helper functions available, it becomes easy to explain the algorithm while showing the code for it as I go.
Essentially, each plane on the original solid represents a single polygon with n sides. So we start with one plane and go from there. We then check every other plane for intersection with the first plane, using CIntersect::TwoPlanes(). Each plane that intersects with the first plane is most likely a side to the final polygon. There are cases where a second plane will intersect the first plane without actually contributing a line segment to the final polygon, but that is handled in a post-processing step later.
The code for starting with a given face and finding each 2nd plane follows.
/**
* Gets the edges for a given polygon. If the polygon is not NULL, the edges are added to it as they are found.
*
* \param _pp3hPoly The polygon to which to add edges. If NULL, no edges are added.
* \param _sSolid The solid containing all of the faces that will be used to find the edges.
* \param _ui32Face The face on the solid to be converted to a polygon.
* \return Returns the number of edges found for the given face on the given solid.
*/
LSUINT32 LSE_CALL CTrisFromSolids::GetPolyEdges( CPolygon3High * _pp3hPoly, const CSolid &_sSolid, LSUINT32 _ui32Face ) {
LSUINT32 ui32Total = 0UL;
// Check all other planes aside from the one given.
for ( LSUINT32 I = 0UL; I < _sSolid.Planes().Length(); ++I ) {
if ( I == _ui32Face ) { continue; }
CRay3High r3hRay;
if ( CIntersect::TwoPlanes<LSDOUBLE, CPlane3High, CRay3High>( _sSolid.Planes()[_ui32Face].phPlane, _sSolid.Planes()[I].phPlane, r3hRay ) ) {
_ui32Face here is the first plane. This code then seeks all 2nd planes. Note that CPolygon3High is basically an array of line segments. In my implementation, for speed, a polygon is told it will have a maximum number of sides, then it allocates those sides from a stack allocator, and then this function will fill in those sides. Which basically means this function has to be called twice. Once to find out how many sides on the polygon, then again to put those sides into the polygon. While it may seem slow, in practice, this is the fastest way to go, rather than having each polygon use a variable-sized std::vector of sides. A stack allocator provides instant allocation of memory, with the loss of any ability to deallocate or reallocate that memory. It is all freed in one sweep when the stack allocator is destroyed (by which point you must also ensure that anything using that memory is already destroyed and dead). Due to these limitations, you need to know before-hand how much to allocate. It turns out that doing this math twice, plus eliminating deallocation time, is actually vastly faster than otherwise. I have a .MAP file with over 30,000 solids, all of which have about 6 polygons, for a total of 180,000 polygons, and in turn 360,000 calls to this routine. It finishes in less than 0.5 seconds. If all of those calls results in allocations, you would have much less RAM and the total time would likely be more than 15 seconds, including deallocation.
Having found a second plane, we now need to find point on that plane. The objective is to find the start point p and the end point q that create the shortest line segment. We do this by searching over all 3rd planes that intersect both of the first 2 planes. The following image shows the ray (purple) for the 2 planes that have intersected, as well as 2 other planes that intersect both of the first 2 planes. These are the 3rd planes—one in yellow and one in green. Both of the 3rd planes have their normals represented by a red arrow.
Both the yellow and green planes form a 3rd plane, and this a point on the current edge of the polygon, but how do we know which point is the p and which is the q? If the plane is facing in the same direction as the ray, it is an end point q, otherwise it is a start point p. We scan for the q that is closest to p, and the p that is closest to q. While this sounds complicated, it is nothing more than 2 dot products. One tells us if it is a p or a q, and the other tells us how for in the direction of the ray the point is. The code follows.
LSBOOL bLeftFound = false, bRightFound = false;
LSDOUBLE dDistLeft = 0.0, dDistRight = 0.0;
CLineSeg3High ls3hThisSeg( CVector3High( 0.0, 0.0, 0.0 ), CVector3High( 0.0, 0.0, 0.0 ) );
// Find a 3rd plane that intersects this point.
for ( LSUINT32 J = 0UL; J < _sSolid.Planes().Length(); ++J ) {
if ( J == I || J == _ui32Face ) { continue; }
CVector3High v3hIntersect;
if ( CIntersect::ThreePlanes<LSDOUBLE, CPlane3High, CVector3High>( _sSolid.Planes()[_ui32Face].phPlane, _sSolid.Planes()[I].phPlane, _sSolid.Planes()[J].phPlane, v3hIntersect ) ) {
LSDOUBLE dDir = _sSolid.Planes()[J].phPlane.n * r3hRay.dir;
LSDOUBLE dDist = r3hRay.dir * v3hIntersect;
if ( dDir > 0.0 ) {
// Right side.
if ( !bRightFound || dDist < dDistRight ) {
dDistRight = dDist;
bRightFound = true;
ls3hThisSeg.q = v3hIntersect;
}
}
else {
dDist = -dDist;
// Left side.
if ( !bLeftFound || dDist < dDistLeft ) {
dDistLeft = dDist;
bLeftFound = true;
ls3hThisSeg.p = v3hIntersect;
}
}
}
}
if ( !bLeftFound || !bRightFound ) { continue; }
if ( _pp3hPoly ) {
_pp3hPoly->Segments()[ui32Total] = ls3hThisSeg;
}
++ui32Total;
}
}
return ui32Total;
}
Remember that the * operator, used to get dDir and dDist, is a vector dot product. Update: Since I reversed the direction of the .MAP planes, dDir < 0.0 became dDir > 0.0, and the line-segment’s p and q were swapped from my original posting of this (to the current code shown here).
As I have explained, in my implementation, this is repeated twice—once to get the total sides on the polygon, and again to actually fill in those sides. Given a solid, the loop looks like this:
// For each face, find out how many edges there are, then add the edges.
for ( LSUINT32 I = m_ui32TotalPolies; I--; ) {
LSUINT32 ui32Total = GetPolyEdges( NULL, _sSolid, I );
if ( !m_pp3hPolygons[I].SetTotalSides( ui32Total, _psaAllocator ) ) { return false; }
GetPolyEdges( &m_pp3hPolygons[I], _sSolid, I );
if ( !m_pp3hPolygons[I].Finalize( 0.0001 ) ) { return false; }
m_pp3hPolygons[I].Plane() = _sSolid.Planes()[I].phPlane;
}
m_ui32TotalPolies here is the same as the number of sides on the solid, which for our cube example is 6. Note that I count down to 0 instead of starting at 0 and going up. This allows each iteration of the for () loop to compare against 0 instead of against m_ui32TotalPolies, which is basically a very minor optimization. The output code is smaller and comparing against 0 is always the fastest compare there is. Smaller code means fewer instruction cache misses as well.
Notice as well that I set the normal of the polygon to the normal of the solid face. Due to rounding errors, we might get a polygon with some vertices exactly on this plane, slightly in front of it, or slightly behind it. When you set the normal for a polygon you have 2 ways of doing it. Either set the normal based off the object that created it, or by calculating the normals of all the triangles in the polygon and reaching an average. At this point we don’t even have triangles, but aside from that it is simply more robust to set the normal of the polygon to match the normal of the face from which it was created.
What Does CPolygon3High::Finalize() Do?
As mentioned, it is possible for the previous routine to add segments to a polygon that don’t actually belong. These can be handled easily by a post-processing routine, which in my case is a call to Finalize(). It basically removes any segments that don’t make sense, and then sequence the remaining segments so that every end point matches a starting point of another segment. Segments that don’t make sense are those that either don’t have a connection on both ends or are shorter than epsilon in length. The code is fairly straight-forward:
/**
* Finalizes the polygon such that the end of each segment connects to the start of another segment.
* If false is returned, at least one segment was unable to be connected.
*
* \param _tEpsilon The epsilon for snapping points together.
* \return Returns true if all end points of the polygon's edges connect with 1 starting point.
*/
LSBOOL LSE_CALL Finalize( _tType _tEpsilon ) {
assert( m_ui32Total >= 3UL );
_tSeg3Type tTemp;
// Remove any segments that have any missing connections.
for ( LSUINT32 I = 0UL; I < m_ui32Total; ) {
// Check P against Q.
LSBOOL bHasP = false, bHasQ = false;
_tType tLen = (m_ptSegs[I].q - m_ptSegs[I].p).LenSq();
if ( tLen >= _tEpsilon * _tEpsilon ) {
for ( LSUINT32 J = 0UL; J < m_ui32Total; ++J ) {
if ( J == I ) { continue; }
_tType tDist = (m_ptSegs[I].p - m_ptSegs[J].q).Len();
if ( tDist <= _tEpsilon ) {
bHasP = true;
break;
}
}
if ( bHasP ) {
// Check its Q.
for ( LSUINT32 J = 0UL; J < m_ui32Total; ++J ) {
if ( J == I ) { continue; }
_tType tDist = (m_ptSegs[I].q - m_ptSegs[J].p).Len();
if ( tDist <= _tEpsilon ) {
bHasQ = true;
break;
}
}
}
}
if ( !bHasP || !bHasQ ) {
Remove( I );
if ( m_ui32Total <= 2UL ) {
return false;
}
}
else {
++I;
}
}
for ( LSUINT32 I = 0UL; I < m_ui32Total; ++I ) {
// Find the starting point that connects to the end point of the Ith edge.
for ( LSUINT32 J = I + 1UL; J < m_ui32Total; ++J ) {
_tType tDist = (m_ptSegs[J].p - m_ptSegs[I].q).Len();
if ( tDist <= _tEpsilon ) {
if ( J != I + 1UL ) { // No need to swap here.
tTemp = m_ptSegs[I+1];
m_ptSegs[I+1] = m_ptSegs[J];
m_ptSegs[J] = tTemp;
}
break;
}
}
}
// Return true if we came full circle.
return (m_ptSegs[0].p - m_ptSegs[m_ui32Total-1].q).Len() <= _tEpsilon;
}
We Now Have a Bunch of Polygons. What Next?
In my case, the CTrisFromSolids class is a 1-to-1 representation of a solid. That is, each solid has a single instance of a CTrisFromSolids class associated with it. That class in turn has one polygon for each face of the solid it represents.
For general-purpose polygons, conversions to triangles means ear-clipping. Luckily, this is only necessary if you have no guarantee that your polygons are convex. In our case, we know all of our polygons are convex, so triangulating our polygons is much simpler. All we have to do is make a triangle list by treating each polygon on each solid as a triangle fan. Although I will present the code for this, keep in mind that at this point our only objective is to get debug visuals that confirm we are on the right track. Don’t spend much time on this routine, and don’t throw away your polygon data yet. You will need it for building your BSP in the next tutorial, which will involved splitting polygons across planes and more fun.
Basically, if you have a bunch of convex polygons, composed of line segments whose starting points are denoted as p, then the following code will export all of the triangles (as a triangle list) to a file. The file is the most basic format for you to load and display to ensure you have the correct results. Remember that in my code, a CTrisFromSolids is the class that represents a single solid, but in polygons rather than planes.
First you need to create vertices from the polygons:
/**
* Generates triangle vertices from its polygon data.
*
* \param _psaAllocator The stack allocator to be used for allocating the vertices.
* \return Returns true if there was enough memory to allocate the vertex data.
*/
LSBOOL LSE_CALL CTrisFromSolids::GenerateTriangles( CStackAllocator * _psaAllocator ) {
if ( !m_psSolid ) { return false; }
// Since all the faces are convex, we don't need to do ear clipping, plus we can easily calculate
// ahead of time the number of triangles there will be.
LSUINT32 ui32Tris = TotalTris() * 3UL;
m_pvVerts = static_cast<LSL_VERTEX *>(_psaAllocator->Alloc( sizeof( LSL_VERTEX ) * ui32Tris, 4UL ));
if ( !m_pvVerts ) { return false; }
LSUINT32 ui32Index = 0UL;
// For each polygon.
for ( LSUINT32 I = m_ui32TotalPolies; I--; ) {
LSUINT32 ui32End = m_pp3hPolygons[I].TotalSegments() - 1UL;
for ( LSUINT32 J = 1UL; J < ui32End; ++J ) {
m_pvVerts[ui32Index].v3hPos = m_pp3hPolygons[I].Segments()[0].p;
m_pvVerts[ui32Index].v3hNormal = -m_pp3hPolygons[I].Plane().n;
m_pvVerts[ui32Index].fUv[0] = m_pvVerts[ui32Index].fUv[1] = 0.0f;
ui32Index++;
m_pvVerts[ui32Index].v3hPos = m_pp3hPolygons[I].Segments()[J+1].p;
m_pvVerts[ui32Index].v3hNormal = -m_pp3hPolygons[I].Plane().n;
m_pvVerts[ui32Index].fUv[0] = m_pvVerts[ui32Index].fUv[1] = 0.0f;
ui32Index++;
m_pvVerts[ui32Index].v3hPos = m_pp3hPolygons[I].Segments()[J].p;
m_pvVerts[ui32Index].v3hNormal = -m_pp3hPolygons[I].Plane().n;
m_pvVerts[ui32Index].fUv[0] = m_pvVerts[ui32Index].fUv[1] = 0.0f;
ui32Index++;
}
}
return true;
}
Then you can run over each solid/CTrisFromSolids object and export the vertex and normal. We have not generated UV coordinates yet, and we won’t be able to do so until far in the future, so just export the vertex and normal for now. Remember, this is just for debugging so that you know you are fine up to this point.
if ( !fsOut.WriteUInt32( ui32Triangles * 3UL ) ) { return LSSTD_E_NODISKSPACE; }
CSolidLeafBspHigh::OutputVertices( slbbBsp.Root(), fsOut );
for ( LSUINT32 I = ui32Solids; I--; ) {
LSUINT32 ui32Total = ptfsTris[I].TotalTris() * 3UL;
for ( LSUINT32 J = 0UL; J < ui32Total; ++J ) {
if ( !fsOut.WriteFloat( static_cast<LSFLOAT>(ptfsTris[I].Verts()[J].v3hPos.x) ) ) { return LSSTD_E_NODISKSPACE; }
if ( !fsOut.WriteFloat( static_cast<LSFLOAT>(ptfsTris[I].Verts()[J].v3hPos.y) ) ) { return LSSTD_E_NODISKSPACE; }
if ( !fsOut.WriteFloat( static_cast<LSFLOAT>(ptfsTris[I].Verts()[J].v3hPos.z) ) ) { return LSSTD_E_NODISKSPACE; }
if ( !fsOut.WriteFloat( static_cast<LSFLOAT>(ptfsTris[I].Verts()[J].v3hNormal.x) ) ) { return LSSTD_E_NODISKSPACE; }
if ( !fsOut.WriteFloat( static_cast<LSFLOAT>(ptfsTris[I].Verts()[J].v3hNormal.y) ) ) { return LSSTD_E_NODISKSPACE; }
if ( !fsOut.WriteFloat( static_cast<LSFLOAT>(ptfsTris[I].Verts()[J].v3hNormal.z) ) ) { return LSSTD_E_NODISKSPACE; }
}
}
fsOut is a file stream here. How you implement this really doesn’t matter. You just need to export the vertices and normals to a file and then load them so that you can see the result.
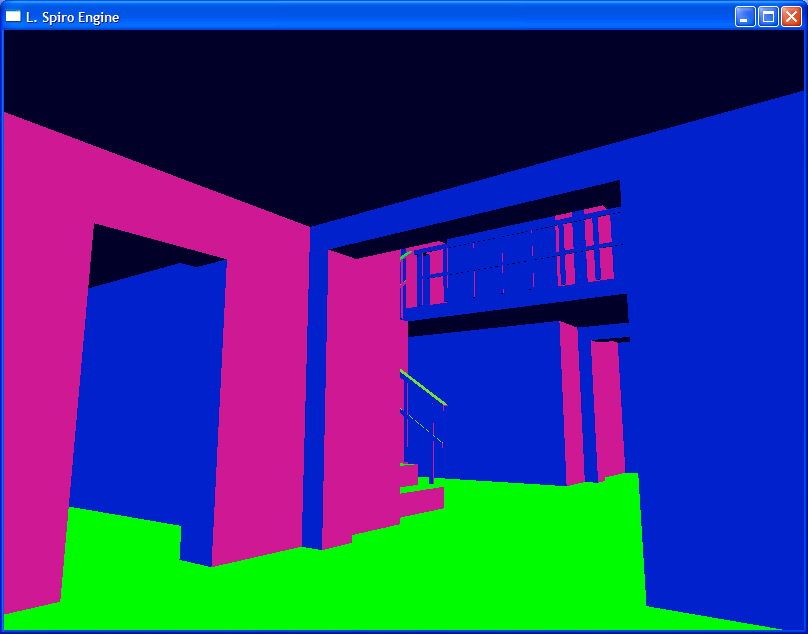
If you have done everything correctly, you should see results such as these:
Conclusion
What? This map seems familiar? I have no idea why.
Today we learned how to get the basic graphics data out of a .MAP file. The polygons—not the triangles—are still necessary for the next tutorial, so don’t throw those away. The graphics data we generated today is only for debug, hence the strange coloring in my final screenshot, but don’t worry—not only will the final screenshots look better than the Worldcraft screenshots, they will also be more functional, and you can include them in your own game projects, with physics as a bonus.
Coming Up
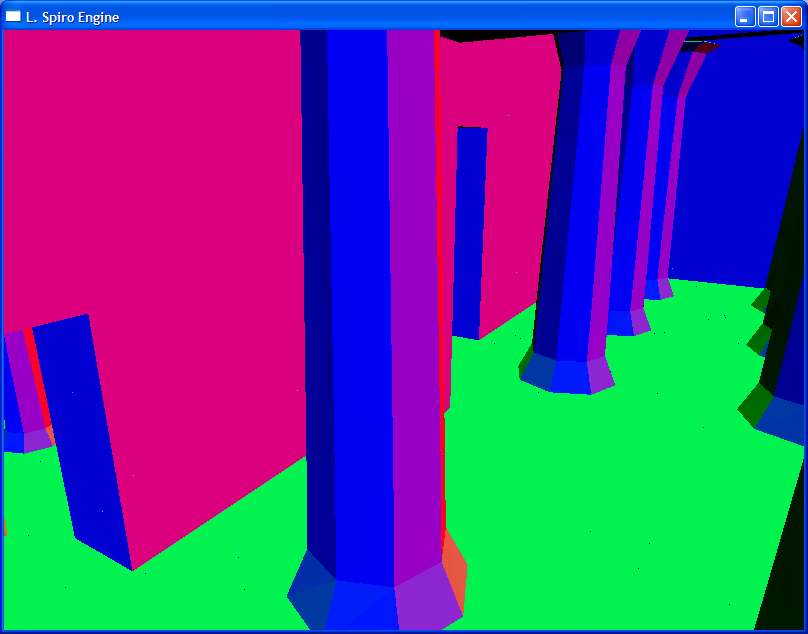
In the next tutorial we will use BSP’s to split our maps into little chunks. Like in the following:
I have no idea why this map would look familiar to anyone, but in any case this was the result of BSP splitting which can’t be detected here. The little specs you can see are basically parts of other solids that are showing through. When we get to hidden surface removal, those will disappear and your triangle counts will decrease significantly. I will explain how to find the optimal triangle count in future tutorials. For now, enjoy what is next to come as you begin loading your own .MAP files. At the end of the tutorials, I will release these GoldenEye 007 .MAP files for you to load an enjoy. But until then, don’t ask how they came into being.
L. Spiro



fantastic tutorial. really inspired me! can’t wait for the rest of the series
I love these tutorial series! I hope there will be more to come!
I was wondering what version of worldcraft are you using as the new hammer is for source.
Thank you. There will be more tutorials, but there will also be a delay for 2 reasons.
#1: My harddrive completely crashed last week and I am still picking up the pieces. I did not lose any engine code, but I have a lot to reinstall. I haven’t even reinstalled Valve Hammer Editor or WorldCraft yet.
#2: I decided to get full DirectX 11 support before I continue on any other part of the engine, because it will be easier to add features if all targets are fully supported. Luckily, I am almost done with that. DirectX 11 is about 95% there.
To answer your question, I am using both Valve Hammer Editor (current version) and WorldCraft 3.3. WorldCraft 3.3 can export .MAP files while Valve Hammer Editor can export .VMF files. Both files are basically the same, but .VMF has some extra features which are easy to handle. In any case, my tutorials can be used with either format. Whether it is .MAP or .VMF, you just have to export the faces of each solid etc. After that, the BSP tree, portal generation, and PVS system work the same, which means you should be able to load Half-Life 2 maps into your own engine by the time my series is done.
L. Spiro