Making Buildings from .MAP Files Part 2

Overview

This is part 2 of my series on loading buildings/interiors/maps from Valve Hammer Editor .MAP files.  Part 1 can be found here.  The purpose of this tutorial is ultimately to generate a convex solid-leaf BSP tree in which each leaf contains at least part of a room.  Generating convex sets of polygons is the first step towards generating portals and later PVS’s.

The Polygon Class Template

The polygon template plays a major role here.  In the last tutorial I explained that it was simply a series of line segments.  I have added new functionality to handle the needs of the conversion process and feel that sample code is now necessary.  Here are the major functions of the polygon template.

	/**
	 * Class CPolygon3Base
	 * \brief A template allowing to create polygons with a variable number of edges.
	 *
	 * Description: A template allowing to create polygons with a variable number of edges.
	 */
	template <typename _tType, typename _tSeg3Type, typename _tPlane3Type>
	class CPolygon3Base {
	public :
		// == Various constructors.
		LSE_CALLCTOR						CPolygon3Base() :
			m_ptSegs( NULL ),
			m_psaAllocator( NULL ),
			m_uiptrUser( 0UL ),
			m_ui32Total( 0UL ) {
		}
		LSE_CALLCTOR						~CPolygon3Base() {
			Reset();
		}

		// == Operators.
		/**
		 * Array access.
		 *
		 * \param _ui32Index The index of the point to be returned.
		 * \return Returns the segment at the given index.
		 */
		_tSeg3Type * LSE_CALL					operator [] ( LSUINT32 _ui32Index ) {
			return &Segments()[_ui32Index];
		}

		/**
		 * Array access.
		 *
		 * \param _ui32Index The index of the point to be returned.
		 * \return Returns the segment at the given index.
		 */
		const _tSeg3Type * LSE_CALL				operator [] ( LSUINT32 _ui32Index ) const {
			return &Segments()[_ui32Index]; operator.
		 *
		 * \param _pSrc The source polygon to copy.
		 * \return Returns a reference to the copied polygon.
		 */
		CPolygon3Base<_tType, _tSeg3Type, _tPlane3Type> & LSE_CALL
									operator = ( const CPolygon3Base<_tType, _tSeg3Type, _tPlane3Type> &_pSrc ) {
			Reset();
			Copy( _pSrc, _pSrc.m_psaAllocator );
			return (*this);
		}

		// == Functions.
		/**
		 * Resets the polygon.
		 */
		LSVOID LSE_CALL						Reset() {
			for ( ; m_ui32Total--; ) {
				m_ptSegs[m_ui32Total].~_tSeg3Type();	// Destroy, don't delete.
			}
			m_ptSegs = NULL;
			m_ui32Total = 0UL;
			m_psaAllocator = NULL;
			m_uiptrUser = 0UL;
		}

		/**
		 * Copies the source polygon into this one.
		 *
		 * \param _p3bSrc The polygon to copy into this one.
		 * \param _psaAllocator The stack allocator to be used for the line segments used by this polygon.
		 * \return Returns true if the segments could be allocated from the given source polygon.
		 */
		LSBOOL LSE_CALL						Copy( const CPolygon3Base<_tType, _tSeg3Type, _tPlane3Type> &_p3bSrc, CStackAllocator * _psaAllocator ) {
			Reset();
			if ( !SetTotalSides( _p3bSrc.TotalSegments(), _psaAllocator ) ) { return false; }
			for ( LSUINT32 I = _p3bSrc.TotalSegments(); I--; ) {
				m_ptSegs[I] = _p3bSrc.Segments()[I];
			}
			m_pPlane = _p3bSrc.m_pPlane;
			m_uiptrUser = _p3bSrc.m_uiptrUser;
			return true;
		}

		/**
		 * Sets the number of segments in the polygon.  This can't be changed after being set once.
		 *
		 * \param _ui32Total The number of segments in the polygon.
		 * \param _psaAllocator The stack allocator to be used for the line segments used by this polygon.
		 * \return Returns true if it was able to allocate the given number of segments from the stack allocator.
		 */
		LSBOOL LSE_CALL						SetTotalSides( LSUINT32 _ui32Total, CStackAllocator * _psaAllocator ) {
			Reset();
			m_psaAllocator = _psaAllocator;
			if ( _ui32Total < 3UL ) { return false; }
			if ( (m_ptSegs = static_cast<_tSeg3Type *>(_psaAllocator->Alloc( sizeof( _tSeg3Type ) * _ui32Total, 4UL ))) ) {
				m_ui32Total = _ui32Total;
				for ( ; _ui32Total--; ) {
					new( &m_ptSegs[_ui32Total] ) _tSeg3Type();
				}
				return true;
			}
			return false;
		}

		/**
		 * Gets the total segments on this polygon.
		 *
		 * \return Returns the total segments on this polygon.
		 */
		LSUINT32 LSE_CALL					TotalSegments() const {
			return m_ui32Total;
		}

		/**
		 * Gets a pointer to the array of segments on this polygon.
		 *
		 * \return Returns a pointer to the array of segments on this polygon, which may be NULL.
		 */
		_tSeg3Type * LSE_CALL					Segments() {
			return m_ptSegs;
		}

		/**
		 * Gets a pointer to the array of segments on this polygon.
		 *
		 * \return Returns a pointer to the array of segments on this polygon, which may be NULL.
		 */
		const _tSeg3Type * LSE_CALL				Segments() const {
			return m_ptSegs;
		}

		/**
		 * Gets the plane for read-only.
		 *
		 * \return Returns the plane for read-only.
		 */
		const _tPlane3Type & LSE_CALL				Plane() const {
			return m_pPlane;
		}

		/**
		 * Gets the plane for read and write.
		 *
		 * \return Returns the plane for read and write.
		 */
		_tPlane3Type & LSE_CALL					Plane() {
			return m_pPlane;
		}

		/**
		 * Sets the user value for the polygon.
		 *
		 * \param _uiptrValue The value to set.
		 */
		LSVOID LSE_CALL						SetUser( LSUINTPTR _uiptrValue ) {
			m_uiptrUser = _uiptrValue;
		}

		/**
		 * Gets the user value.
		 *
		 * \return Returns the user value.
		 */
		LSUINTPTR LSE_CALL					GetUser() const {
			return m_uiptrUser;
		}

		/**
		 * Finalizes the polygon such that the end of each segment connects to the start of another segment.
		 *	If false is returned, at least one segment was unable to be connected.
		 *
		 * \param _tEpsilon The epsilon for snapping points together.
		 * \return Returns true if all end points of the polygon's edges connect with 1 starting point.
		 */
		LSBOOL LSE_CALL						Finalize( _tType _tEpsilon ) {
			assert( m_ui32Total >= 3UL );
			_tSeg3Type tTemp;
			// Remove any segments that have any missing connections.
			for ( LSUINT32 I = 0UL; I < m_ui32Total; ) {
				// Check P against Q.
				LSBOOL bHasP = false, bHasQ = false;
				_tType tLen = (m_ptSegs[I].q - m_ptSegs[I].p).LenSq();
				if ( tLen >= _tEpsilon * _tEpsilon ) {
					for ( LSUINT32 J = 0UL; J < m_ui32Total; ++J ) {
						if ( J == I ) { continue; }
						_tType tDist = (m_ptSegs[I].p - m_ptSegs[J].q).Len();
						if ( tDist <= _tEpsilon ) {
							bHasP = true;
							break;
						}
					}
					if ( bHasP ) {
						// Check its Q.
						for ( LSUINT32 J = 0UL; J < m_ui32Total; ++J ) {
							if ( J == I ) { continue; }
							_tType tDist = (m_ptSegs[I].q - m_ptSegs[J].p).Len();
							if ( tDist <= _tEpsilon ) {
								bHasQ = true;
								break;
							}
						}
					}
				}

				if ( !bHasP || !bHasQ ) {
					Remove( I );
					if ( m_ui32Total <= 2UL ) {
						return false;
					}
				}
				else {
					++I;
				}
			}
			for ( LSUINT32 I = 0UL; I < m_ui32Total; ++I ) {
				// Find the starting point that connects to the end point of the Ith edge.
				for ( LSUINT32 J = I + 1UL; J < m_ui32Total; ++J ) {
					_tType tDist = (m_ptSegs[J].p - m_ptSegs[I].q).Len();
					if ( tDist <= _tEpsilon ) {
						if ( J != I + 1UL ) {	// No need to swap here.
							tTemp = m_ptSegs[I+1];
							m_ptSegs[I+1] = m_ptSegs[J];
							m_ptSegs[J] = tTemp;
						}
						break;
					}
				}
			}

			// Return true if we came full circle.
			return (m_ptSegs[0].p - m_ptSegs[m_ui32Total-1].q).Len() <= _tEpsilon;
		}

		/**
		 * Removes a line segment at the given index.
		 *
		 * \param _ui32Index Index of the line segment to remove.
		 */
		LSVOID LSE_CALL						Remove( LSUINT32 _ui32Index ) {
			if ( _ui32Index < m_ui32Total ) {
				m_ptSegs[_ui32Index].~_tSeg3Type();		// Destroy, don't delete.
				for ( LSUINT32 J = _ui32Index + 1UL; J < m_ui32Total; ++J ) {
					m_ptSegs[J-1] = m_ptSegs[J];
				}
				--m_ui32Total;
			}
		}

	protected :
		// == Members.
		/**
		 * Pointer to the array of line segments.
		 */
		_tSeg3Type *						m_ptSegs;

		/**
		 * The stack allocator used by this object.
		 */
		CStackAllocator *					m_psaAllocator;

		/**
		 * Special meaning.
		 */
		LSUINTPTR						m_uiptrUser;

		/**
		 * Total line segments.
		 */
		LSUINT32						m_ui32Total;

		/**
		 * The plane for this polygon.
		 */
		_tPlane3Type						m_pPlane;

	};

There is nothing particularly Earth-shattering here, but it will be useful to have a reference for when you see these functions called later.  Again, this uses a stack allocator, which provides only Alloc() but is extremely fast.  This means you need to know in advance the maximum number of sides you will have.  If you want to use a regular allocator, the places where I used ~_tSeg3Type() should be replaced with deallocation.  The only detail that probably needs some explanation is the m_uiptrUser member.  It is important for polygons to have a way to separate themselves from other polygons for various reasons.  When merging polygons, you don’t want to merge polygons that are using different materials.  For now, we won’t be merging polygons, but we will be splitting them and we need to keep track of materials for each polygon for future reference.

Hidden-Surface Removal

Before building a BSP tree, it is a good idea to perform hidden-surface removal.  This simply removes polygons that can’t be seen in the final product because they are either entirely inside a solid or entirely coplanar and contained within a face of said solid.  Not only is it faster to remove polygons rather than triangles, it reduces the complexity of the BSP tree and helps increase the size of discovered rooms.  In an average man-made .MAP file, ~30% of the polygons in the scene can be eliminated, which is a significant factor.

In my implementation, solids are loaded into a CSolid class. It contains the planes for each face, the materials for each face, etc. Remember that a solid is just an array of half spaces with the normals pointing outward. In order for the algorithms to work you should ensure that your normals for each solid face are pointing outward, because by default the normals in .MAP files point inward.

The CSolid class is very simple and just looks like this:

	/**
	 * Class CSolid
	 * \brief A solid is always convex and represented by an array of new fewer than 3 half-spaces.
	 *
	 * Description: A solid is always convex and represented by an array of new fewer than 3 half-spaces.
	 */
	class CSolid {
	public :
		// == Various constructors.
		LSE_CALLCTOR					CSolid();

		// == Types.
		/**
		 * A single face of the plane.
		 */
		typedef struct LSL_PLANE_FACE {
			/**
			 * Plane for this face.
			 */
			CPlane3High				phPlane;

			/**
			 * Material for this face.
			 */
			CString					sMaterial;

			/**
			 * Other face properties removed for brevity…
			 */
		} * LPLSL_PLANE_FACE, * const LPCLSL_PLANE_FACE;

		// == Functions.
		/**
		 * Sets the number of faces on the solid.
		 *
		 * \param _ui32Total The total faces to add.
		 * \return Returns true if there was enough memory to set the given number of faces.
		 */
		LSE_INLINE LSBOOL LSE_CALL			SetFaces( LSUINT32 _ui32Total );

		/**
		 * Gets the array of planes that make up this solid for reading only.
		 *
		 * \return Returns a constant reference to the array of planes that make up this solid.
		 */
		LSE_INLINE const CVector<LSL_PLANE_FACE, LSUINT32> & LSE_CALL
								Planes() const;

		/**
		 * Resets the solid to nothing.
		 */
		LSVOID LSE_CALL					Reset();

		/**
		 * Marks the solid as a duplicate of another solid in terms of geometry.
		 */
		LSVOID LSE_CALL					SetAsDuplicate();

		/**
		 * Gets whether or not the solid is a duplicate of another solid in terms of geometry.
		 *
		 * \return Returns true if the solid has been marked as a duplicate.
		 */
		LSBOOL LSE_CALL					IsDuplicate() const;

		/**
		 * Returns true if the geometry of this solid matches the geometry of the input solid.
		 *
		 * \param _sSolid The solid against which to check for matching geometry.
		 * \param _dEpsilon Epsilon.
		 * \return Returns true if both solids are a match in geometry.
		 */
		LSBOOL LSE_CALL					SolidMatchesGeometry( const CSolid &_sSolid, LSDOUBLE _dEpsilon ) const;

	protected :
		// == Members.
		/**
		 * The array of faces that make this solid.
		 */
		CVector<LSL_PLANE_FACE, LSUINT32>		m_vFaces;

		/**
		 * Is this a duplicate?
		 */
		LSBOOL						m_bDuplicate;

	};

A nested structure contains the properties of a single face, and a solid is just an array of those properties.  m_bDuplicate will be explained shortly.

The routine for determining if a polygon is inside a solid or fully occluded by one of its faces is simple: Check for any points on the polygon being outside of the solid.  Since the solid’s normals are all facing towards the outside, this simply means checking for any point on the polygon that classifies as being in front of any face on the solid.

Classifying points in relationship to planes is very simple:

	/**
	 * Classifies a point in relation to a given plane.
	 *
	 * \param _vPoint The point to test against the given plane.
	 * \param _pPlane The plane to test against the given point.
	 * \param _fThickness The thickness of the plane.
	 * \return Returns a plane classification.
	 */
	template <typename _tType, typename _tVec3Type, typename _tPlane3Type>
	static LSE_INLINE LSM_PLANE_INTERSECT LSE_CALL				Point( const _tVec3Type &_vPoint, const _tPlane3Type &_pPlane, _tType _fThickness = static_cast<_tType>(LSM_PLANE_THICKNESS) ) {
		_tType fDist = (_pPlane.n * _vPoint) - _pPlane.dist;
		if ( fDist > _fThickness ) { return LSM_PI_FRONT; }
		if ( fDist < -_fThickness ) { return LSM_PI_BACK; }
		return LSM_PI_COPLANAR;
	}

And with that utility function, we can check for polygons inside solids.  Note that only LSM_PI_FRONT is checked, which means points on the surface of the solid also count as being inside, and this is what we want.
Again note that the vector * operator is a dot product.

	/**
	 * Determines if the given polygon fits entirely inside the given solid.
	 *
	 * \param _p3hPoly The polygon to check for fitting entirely inside the given solid.
	 * \param _sSolid The given solid.
	 * \param _dEpsilon Epsilon for testing.
	 * \return Returns true if the given polygon fits entirely inside the given solid.
	 */
	LSBOOL LSE_CALL CTrisFromSolids::PolyIsInSolid( const CPolygon3High &_p3hPoly, const CSolid &_sSolid, LSDOUBLE _dEpsilon ) {
		if ( _sSolid.Planes().Length() < 3UL ) { return false; }
		// If no points in the polygon are on the front side of any of the faces of the solid, the polygon is inside the solid.
		for ( LSUINT32 I = _sSolid.Planes().Length(); I--; ) {
			for ( LSUINT32 J = _p3hPoly.TotalSegments(); J--; ) {
				if ( CClassify::Point( _p3hPoly[J]->p, _sSolid.Planes()[I].phPlane, _dEpsilon ) == LSM_PI_FRONT ) { return false; }
			}
		}
		return true;
	}

CTrisFromSolids is my class for representing a solid via just polygons which will later be copied, split, and converted to triangles.  Next we want to call the above function and “eliminate” polygons that are hidden.  First the function that actually creates polygons from solids:

	/**
	 * Creates an array of triangles for visualization of the given solid.
	 *
	 * \param _sSolid The solid to convert to triangles.
	 * \param _psaAllocator The stack allocator to be used to make the array of polygons and for the polygons
	 *	to use for their allocations.
	 * \return Returns true if there was enough memory to perform the conversion.
	 */
	LSBOOL LSE_CALL CTrisFromSolids::MakeTriangles( const CSolid &_sSolid, CStackAllocator * _psaAllocator ) {
		m_psSolid = &_sSolid;
		m_pp3hPolygons = static_cast<CPolygon3High *>(_psaAllocator->Alloc( sizeof( CPolygon3High ) * _sSolid.Planes().Length(), 4UL ));
		if ( !m_pp3hPolygons ) { return false; }
		m_ui32TotalPolies = _sSolid.Planes().Length();
		for ( LSUINT32 I = m_ui32TotalPolies; I--; ) {
			new( &m_pp3hPolygons[I] ) CPolygon3High();
		}

		// For each face, find out how many edges there are, then add the edges.
		for ( LSUINT32 I = m_ui32TotalPolies; I--; ) {
			LSUINT32 ui32Total = GetPolyEdges( NULL, _sSolid, I );
			if ( !m_pp3hPolygons[I].SetTotalSides( ui32Total, _psaAllocator ) ) { return false; }
			GetPolyEdges( &m_pp3hPolygons[I], _sSolid, I );
			if ( !m_pp3hPolygons[I].Finalize( 0.0001 ) ) { return false; }
			m_pp3hPolygons[I].Plane() = _sSolid.Planes()[I].phPlane;
			m_pp3hPolygons[I].SetUser( reinterpret_cast<LSUINTPTR>(&_sSolid.Planes()[I]) );
		}

		return true;
	}

Then the function for removing occluded polygons:

	/**
	 * Marks all polygons on this mesh object that are occluded by any faces on any solids in the given array of solids.
	 *	The array should be the same copy from which _sSolid came in the original call to MakeTriangles().
	 *
	 * \param _psSolids Pointer to an array of solids.
	 * \param _ui32Total Total solids in the array.
	 * \param _dEpsilon Epsilon.
	 */
	LSVOID LSE_CALL CTrisFromSolids::RemoveOccludedPolies( const CSolid * _psSolid, LSUINT32 _ui32Total, LSDOUBLE _dEpsilon ) {
		while ( _ui32Total-- ) {
			if ( &_psSolid[_ui32Total] == m_psSolid || _psSolid[_ui32Total].Planes().Length() < 3UL || _psSolid[_ui32Total].IsDuplicate() ) { continue; }

			for ( LSUINT32 I = TotalPolygons(); I--; ) {
				if ( PolyIsInSolid( m_pp3hPolygons[I], _psSolid[_ui32Total], _dEpsilon ) ) {
					// Don't actually remove it.  Just mark it.
					m_pp3hPolygons[I].SetUser( 0 );
				}
			}
		}
	}

A few notes:

• MakeTriangles() is the function that actually creates one polygon per face on a given solid.  The CTrisFromSolids member m_psSolid is a record of the solid used to make the CTrisFromSolids object, and here it is used to make sure the original solid is not used to perform hidden-polygon removal on this object, because doing so would eliminate all polygons on the object.
• Invalid solids are also not checked.
• Duplicate solids are not checked.  Because they are duplicates, checking them would be the same as checking the original solid from which this object was built.
• Polygons are not actually removed from the object, they are just marked as having no material (recall that we set the user property of a polygon to a pointer to the original solid face from which it was created).

Finally, we need to know which solids are duplicates.  This is simple, as they will have the same number of faces and each plane on one solid will have a match on the other solid.

	/**
	 * Returns true if the geometry of this solid matches the geometry of the input solid.
	 *
	 * \param _sSolid The solid against which to check for matching geometry.
	 * \param _dEpsilon Epsilon.
	 * \return Returns true if both solids are a match in geometry.
	 */
	LSBOOL LSE_CALL CSolid::SolidMatchesGeometry( const CSolid &_sSolid, LSDOUBLE _dEpsilon ) const {
		// All faces on this must have exactly one matching face on the other.
		if ( m_vFaces.Length() != _sSolid.m_vFaces.Length() ) { return false; }
		for ( LSUINT32 I = m_vFaces.Length(); I--; ) {
			LSBOOL bMatch = false;
			for ( LSUINT32 J = _sSolid.m_vFaces.Length(); J--; ) {
				if ( ::fabs( m_vFaces[I].phPlane.dist - _sSolid.m_vFaces[J].phPlane.dist ) > _dEpsilon ) { continue; }
				if ( ::fabs( m_vFaces[I].phPlane.n.x - _sSolid.m_vFaces[J].phPlane.n.x ) > _dEpsilon ) { continue; }
				if ( ::fabs( m_vFaces[I].phPlane.n.y - _sSolid.m_vFaces[J].phPlane.n.y ) > _dEpsilon ) { continue; }
				if ( ::fabs( m_vFaces[I].phPlane.n.z - _sSolid.m_vFaces[J].phPlane.n.z ) > _dEpsilon ) { continue; }
				bMatch = true;
				break;
			}
			if ( !bMatch ) { return false; }
		}
		return true;
	}

Workflow Until Now
For the first time I will present the overall workflow for the process until now.

		/**** LOAD .MAP DATA SOLIDS INTO ARRAY CALLED lLevel.Solids() ****/

		// Remove duplicate solids.
		LSUINT32 ui32Duplicates = 0UL;
		for ( LSUINT32 I = lLevel.Solids().Length(); I--; ) {
			for ( LSUINT32 J = I + 1UL; J < lLevel.Solids().Length(); ++J ) {
				if ( lLevel.Solids()[I].SolidMatchesGeometry( lLevel.Solids()[J], LSL_EPSILON ) ) {
					lLevel.Solids()[J].SetAsDuplicate();
					++ui32Duplicates;
					break;
				}
			}
		}

		CStackAllocator saStackAllocator;
		::printf( "%u solids loaded.  Creating triangle meshes.\r\n", ui32Solids );
		{
			CTrisFromSolids * ptfsTris = static_cast<CTrisFromSolids *>(saStackAllocator.Alloc( sizeof( CTrisFromSolids ) * ui32Solids ));
			for ( LSUINT32 I = ui32Solids; I--; ) {
				new( &ptfsTris[I] ) CTrisFromSolids();
			}

			LSUINT32 ui32Invalids = 0UL;
			LSUINT32 ui32Triangles = 0UL;
			LSUINT32 ui32Polygons = 0UL;
			for ( LSUINT32 I = ui32Solids; I--; ) {
				if ( lLevel.Solids()[I].IsDuplicate() ) { continue; }
				if ( !ptfsTris[I].MakeTriangles( lLevel.Solids()[I], &saStackAllocator ) ) {
					// The solid is invalid but life goes on.  Just remove it and continue.
					++ui32Invalids;
					ptfsTris[I].Reset();
					lLevel.Solids()[I].Reset();
				}
				else {
					ui32Polygons += ptfsTris[I].TotalPolygons();
				}
			}
			if ( ui32Invalids ) {
				::printf( "%u solid(s) invalid.\r\n", ui32Invalids );
			}
			::printf( "%u polygons.  Removing hidden polygons.\r\n", ui32Polygons );
			LSUINT32 ui32TotalPoliesAfterOcc = 0UL;
			for ( LSUINT32 I = ui32Solids; I--; ) {
				if ( ptfsTris[I].TotalPolygons() ) {	// If the solid is invalid, this will be 0.
					ptfsTris[I].RemoveOccludedPolies( &lLevel.Solids()[0], lLevel.Solids().Length(), 0.0/*LSM_DBL_EPSILON*/ );
					for ( LSUINT32 J = ptfsTris[I].TotalPolygons(); J--; ) {
						if ( ptfsTris[I].Polygons()[J].GetUser() ) {
							ui32Triangles += ptfsTris[I].Polygons()[J].TotalSegments() - 2UL;
							++ui32TotalPoliesAfterOcc;
						}
					}
				}
			}

We start by creating an array of solids loaded from the .MAP file. Then we tag duplicates. We do this first to avoid generating duplicate polygonal meshes from the start. Then we allocate one CTrisFromSolids for each CSolid there is, though you could allocate only enough for the non-duplicate ones.
When generating the polygons, we skip duplicated solids and keep track of invalid solids but don’t abort. Aborting over such a thing is nothing but an annoyance to users. The printed message tells the mappers that there is a problem, but without getting into the level and seeing a blank spot somewhere in the map it is pretty hard to tell where exactly the problem is.
Finally, after non-duplicate solids are converted to polygonal form, each polygon is checked for being hidden and removed if so. ui32TotalPoliesAfterOcc counts the total polygons left after removal.

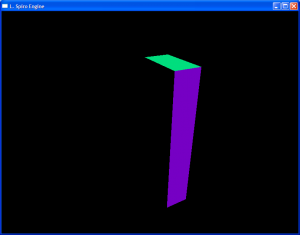
This would be a good time to check that your results are as expected.  This is easy with a simple test scene such as the following:

By positioning the camera inside the larger box, we can see that the face of the smaller box that connects to the larger box has been removed.

BSP Generation

The concept of what BSP’s are and do is widely documented, and if you aren’t familiar with these ideas then it is unlikely this tutorial is really meant for you.  The type of BSP tree we will create is called a solid-leaf BSP.  There are only 3 major steps in the construction of such a tree:

• Pick the best splitting plane.
• Classify polygons according to the split plane.
• Split polygons that intersect the split plane.

Picking the best splitting plane means iterating over the existing planes in the list of polygons and performing a weighted analysis that leverages the cost of splitting polygons vs. having a balanced tree.  A balanced tree is one in which there is a fairly equal number of polygons on each side of the splitting plane.  Fewer splitting planes is good, and having similar numbers of polygons on each side of the plane is good.  The following function is what I use to evaluate the quality of a splitting plane.  While equations differ from implementation to implementation, a common theme is that the lower scores are better than higher scores.  And since these scores tend to need tweaking, easily-modifiable weight are used in the formula.  Here is my function for picking the best splitting plane:

		/**
		 * Finds the best splitting plane for the given set of input polygons.
		 *
		 * \param _vPolies The polygons for which to find the best splitting plane.
		 * \param _ui32Index On return, holds the index of the polygon whose plane was used for the return.
		 * \param _fThickness Plane thickness.
		 * \return Returns the best plane for splitting the given set of polygons.
		 */
		_tPlaneType LSE_CALL				BestSplittingPlane( const CVector<_tPolyType, LSUINT32, 4096UL> &_vPolies, LSUINT32 &_ui32Index, _tType _fThickness = static_cast<_tType>(LSM_PLANE_THICKNESS) ) {
			// Blend factor for optimizing for balancing splits (to be tweaked).
			_tType fK = static_cast<_tType>(0.8);

			// Variables for tracking the best plane seen so far.
			_tPlaneType pBest;
			_tType fBestScore = static_cast<_tType>(LSM_INFINITY);	// Lower score = better.
			LSBOOL bFoundOneBest = false;

			// Compare every plane against every other plane.
			for ( LSUINT32 I = 0UL; I < _vPolies.Length(); ++I ) {
				LSUINT32 ui32Front = 0, ui32Behind = 0, ui32Straddling = 0;
				const _tPlaneType & pPlane = _vPolies[I].Plane();
				if ( bFoundOneBest && pBest == pPlane ) { continue; }

				// Check against all other polygons.  See how many are in front,
				//	behind, or straddling.
				for ( LSUINT32 J = 0UL; J < _vPolies.Length(); ++J ) {
					if ( I == J ) { continue; }

					switch ( CClassify::Polygon( _vPolies[J], pPlane, _fThickness ) ) {
						case LSM_PI_COPLANAR : {
							// Send these down the front by falling through.
						}
						case LSM_PI_FRONT : {
							++ui32Front;
							break;
						}
						case LSM_PI_BACK : {
							++ui32Behind;
							break;
						}
						case LSM_PI_INTERSECT : {
							++ui32Straddling;
							break;
						}
					}
				}

				// Get the score for this plane.
				_tType fScore = fK * ui32Straddling + (static_cast<_tType>(1.0) - fK) * CMathLib::AbsT<_tType>( static_cast<_tType>(ui32Front - ui32Behind) );
				if ( fScore < fBestScore ) {
					fBestScore = fScore;
					pBest = pPlane;
					bFoundOneBest = true;
					_ui32Index = I;
				}
			}
			return pBest;
		}

This is a member of my templated CSolidLeafBspBase class.  I have chosen a weight of 0.8, which means splitting polygons accounts for 80% of the final score while balanced trees account for 20%.  Since higher scores are bad, more splits equates to a worse score.  For the work I have done so far, this has served me well, but I have not yet taken the time to find the best possible value for this weight since my current focus is on getting the final result, so don’t take my value as the best possible value there is.  Feel free to experiment with this weight.

With that out of the way, the overall BSP generation routine can be presented.  This follows the same BSP pseudo-code you can find almost anywhere online, and there is nothing fancy here except the use of explicit stacks.

		/**
		 * Builds the BSP given an array of polygons in which the leafs store convex sets of polygons rather than
		 *	just polygons coplanar to the leaf plane.
		 *
		 * \param _ppPolies The array of polygons.
		 * \param _ui32Total The total number of polygons.
		 * \param _psaAllocator The stack allocator to be used to allocate new nodes and polygon segments.
		 * \param _fThickness Plane thickness.
		 * \return Returns true if there was enough memory to create the BSP tree.
		 */
		LSBOOL LSE_CALL						CreateBspConvex( const _tPolyType * _ppPolies, LSUINT32 _ui32Total,
			CStackAllocator * _psaAllocator, _tType _fThickness = static_cast<_tType>(LSM_PLANE_THICKNESS) ) {
			// Make a copy of the polygons.
			CVector<_tPolyType, LSUINT32, 4096UL> vPolyCopy;
			vPolyCopy.Allocate( _ui32Total );
			for ( LSUINT32 I = 0UL; I < _ui32Total; ++I ) {
				if ( _ppPolies[I].TotalSegments() ) {
					if ( !vPolyCopy.Push( _tPolyType() ) ) { return false; }
					if ( !vPolyCopy[vPolyCopy.Length()-1UL].Copy( _ppPolies[I], _psaAllocator ) ) { return false; }
				}
			}
			vPolyCopy.Snap();

			return CreateBspConvex( m_nRoot, vPolyCopy, _psaAllocator, _fThickness );
		}

		/**
		 * Builds the BSP given an array of polygons and the node in which to store the results
		 *
		 * \param _nNode The node in which to store the results of the splitting.
		 * \param _vPolies The array of polygons.
		 * \param _psaAllocator The stack allocator to be used to allocate new nodes and polygon segments.
		 * \param _fThickness Plane thickness.
		 * \return Returns true if there was enough memory to create the BSP tree.
		 */
		LSBOOL LSE_CALL						CreateBspConvex( LSP_NODE &_nNode, const CVector<_tPolyType, LSUINT32, 4096UL> &_vPolies,
			CStackAllocator * _psaAllocator, _tType _fThickness = static_cast<_tType>(LSM_PLANE_THICKNESS) ) {
			// Explicit stacking is used for stability.  Stack overflow on large/complicated next-generation maps is not
			//	a problem for this algorithm.
			CVector<LSP_STACK, LSUINT32, 4096UL> vStack;
			vStack.Allocate( _vPolies.Length() );	// The number of polygons should be sufficient stack size.

			// Start it off with the first node.
			if ( !vStack.Push( LSP_STACK() ) ) { return false; }
			vStack[0].pnNode = &_nNode;
			vStack[0].vPolies = _vPolies;

			CVector<_tPolyType, LSUINT32, 4096UL> vFrontPolies, vBackPolies;
			while ( vStack.Length() ) {
				LSP_STACK sThis = vStack[vStack.Length()-1UL];
				vStack.PopNoDealloc();
				if ( sThis.vPolies.Length() == 0UL ) { continue; }
				vFrontPolies.ResetNoDealloc();
				vBackPolies.ResetNoDealloc();
				LSUINT32 ui32Index;
				sThis.pnNode->tPlane = BestSplittingPlane( sThis.vPolies, ui32Index, _fThickness );

				for ( LSUINT32 I = 0UL; I < sThis.vPolies.Length(); ++I ) {
					if ( I == ui32Index ) {
						if ( !sThis.pnNode->vPolies.Push( sThis.vPolies[I] ) ) {
							return false;
						}
						continue;
					}
					switch ( CClassify::Polygon( sThis.vPolies[I], sThis.pnNode->tPlane, _fThickness ) ) {
						case LSM_PI_FRONT : {
							if ( !vFrontPolies.Push( sThis.vPolies[I] ) ) { return false; }
							break;
						}
						case LSM_PI_BACK : {
							if ( !vBackPolies.Push( sThis.vPolies[I] ) ) { return false; }
							break;
						}
						case LSM_PI_COPLANAR : {
							if ( !sThis.pnNode->vPolies.Push( sThis.vPolies[I] ) ) {
								return false;
							}
							break;
						}
						case LSM_PI_INTERSECT : {
							LSUINT32 ui32Left, ui32Right;
							CPhysUtils::Split<_tType, _tVecType, _tPolyType, _tPlaneType>( sThis.vPolies[I], sThis.pnNode->tPlane, &ui32Left, NULL, &ui32Right, NULL,
								_fThickness );
							_tPolyType tLeft, tRight;
							if ( !tLeft.SetTotalSides( ui32Left, _psaAllocator ) ) {
								return false;
							}
							if ( !tRight.SetTotalSides( ui32Right, _psaAllocator ) ) {
								return false;
							}
							CPhysUtils::Split<_tType, _tVecType, _tPolyType, _tPlaneType>( sThis.vPolies[I], sThis.pnNode->tPlane, NULL, &tLeft, NULL, &tRight,
								_fThickness );
							if ( !vFrontPolies.Push( tLeft ) ) { return false; }
							if ( !vBackPolies.Push( tRight ) ) { return false; }
							break;
						}
					}
				}

				sThis.pnNode->vPolies.Snap();
				if ( vFrontPolies.Length() ) {
					sThis.pnNode->pnFront = static_cast<LSP_NODE *>(_psaAllocator->Alloc( sizeof( LSP_NODE ), 4UL ));
					if ( !sThis.pnNode->pnFront ) {
						return false;
					}
					new( sThis.pnNode->pnFront ) LSP_NODE();
					if ( !vStack.Push( LSP_STACK() ) ) {
						return false;
					}
					sThis.pnNode->pnFront->pnParent = sThis.pnNode;
					vStack[vStack.Length()-1].pnNode = sThis.pnNode->pnFront;
					vStack[vStack.Length()-1].vPolies = vFrontPolies;
				}
				if ( vBackPolies.Length() ) {
					sThis.pnNode->pnBack = static_cast<LSP_NODE *>(_psaAllocator->Alloc( sizeof( LSP_NODE ), 4UL ));
					if ( !sThis.pnNode->pnBack ) {
						return false;
					}
					new( sThis.pnNode->pnBack ) LSP_NODE();
					if ( !vStack.Push( LSP_STACK() ) ) {
						return false;
					}
					sThis.pnNode->pnBack->pnParent = sThis.pnNode;
					vStack[vStack.Length()-1].pnNode = sThis.pnNode->pnBack;
					vStack[vStack.Length()-1].vPolies = vBackPolies;
				}
			}
			return true;
		}

As with any standard BSP tree, the best splitting plane is chosen and each polygon is then classified as being in front of, behind, coplanar to, or intersecting that plane and treated accordingly.  Logically, anything on the same plane should be sent to the current tree node, anything in front of it should be sent to the “front” child node, anything behind it should be sent to the “back” child node, and anything intersecting it should be split and sent to both the front and back nodes.  A node is a nested structure which looks like this:

		/**
		 * A node in the BSP tree.
		 */
		typedef struct LSP_NODE {
			/**
			 * The parent node.
			 */
			LSP_NODE *					pnParent;

			/**
			 * The front node.
			 */
			LSP_NODE *					pnFront;

			/**
			 * The back node.
			 */
			LSP_NODE *					pnBack;

			/**
			 * The array of polygons.
			 */
			CVector<_tPolyType, LSUINT32, 4096UL>
									vPolies;

			/**
			 * The plane.
			 */
			_tPlaneType					tPlane;

			// == Various constructors.
			LSE_CALLCTOR					LSP_NODE() :
				pnParent( NULL ),
				pnFront( NULL ),
				pnBack( NULL ) {
			}
			LSE_CALLCTOR					~LSP_NODE() {
				if ( pnFront ) {
					pnFront->~LSP_NODE();
					pnFront = NULL;
				}
				if ( pnBack ) {
					pnBack->~LSP_NODE();
					pnBack = NULL;
				}
			}
		} * LPLSP_NODE, * const LPCLSP_NODE;

For now the parent nodes are not needed, but they will be in future tutorials.  Notice how nodes do not delete their children.  That is because they were allocated from a stack allocator for speed.  If you are using regular allocation, the places where I called ~LSP_NODE() are the places where you would delete the children nodes instead.  Again I have to highly recommend the use of a stack allocator not only for its allocation speed (which is impossible to beat by any other form of allocator) but also its clean-up speed which is also virtually instantaneous.  Not to mention that there is n0 book-keeping for any given allocation, so memory is also heavily conserved.

Of course, to classify polygons to a plane we need another CClassify helper function.  To classify a polygon with a plane is fairly simple.  Classify each point on the polygon and you can determine if all are in front, all behind, all coplanar, or anything else as intersecting.

		/**
		 * Classifies a polygon in relation to a given plane.
		 *
		 * \param _pPoly The polygon to test against the given plane.
		 * \param _pPlane The plane to test against the given point.
		 * \param _fThickness The thickness of the plane.
		 * \return Returns a plane classification.
		 */
		template <typename _tType, typename _tPoly3Type, typename _tPlane3Type>
		static LSE_INLINE LSM_PLANE_INTERSECT LSE_CALL				Polygon( const _tPoly3Type &_pPoly, const _tPlane3Type &_pPlane, _tType _fThickness = static_cast<_tType>(LSM_PLANE_THICKNESS) ) {
			LSUINT32 ui32Front = 0UL, ui32Back = 0UL;

			// Easy as pie.  Loop over vertices and determine if all are on one side or not.
			for ( LSUINT32 I = _pPoly.TotalSegments(); I--; ) {
				switch ( Point<_tType>( _pPoly[I]->p, _pPlane, _fThickness ) ) {
					case LSM_PI_FRONT : {
						// This one is in front.  If any are in back then we are straddling.
						if ( ui32Back ) { return LSM_PI_INTERSECT; }
						++ui32Front;
						break;
					}
					case LSM_PI_BACK : {
						// This one is in back.  If any are in front then we are straddling.
						if ( ui32Front ) { return LSM_PI_INTERSECT; }
						++ui32Back;
						break;
					}
				}
			}
			// We are not straddling.  Then we must be fully in front, fully behind, or coplanar.
			if ( ui32Front ) { return LSM_PI_FRONT; }
			return ui32Back ? LSM_PI_BACK : LSM_PI_COPLANAR;
		}

As a tiny optimization, the last return avoids branching.

The last major step is to split polygons that intersect the splitting plane.  In some BSP implementations, the same polygon is just sent down to both sides of the children nodes, but that will not work for our needs.  But splitting polygons is very little effort, so if you have never done it before don’t panic.  The idea is simple: Run over the line segments in a polygon and each time the line segments classify as being in front of the plane, add the whole segment to the front polygon.  When they classify as being behind the plane, add the whole segment to the back polygon.  And when they intersect the plane, add one part to the front and one part to the end.

2 notable points about my implementation though:

• Again I am using stack allocators, so I have to run the test once to get the totals for each side and again to get the actual line segments for each side.
• My workflow ensures that my polygon’s line segments’ end points meet up with a start-point for the next line-segment, so for this routine I only need to add start points for each line segment and then afterwards connect each end point to the next segment’s start point.

The routine for splitting a polygon then is as follows:

		/**
		 * Splits a polygon into 2 new polygons along a given plane.
		 *
		 * \param _pPoly The polygon to split.
		 * \param _pPlane The plane along which to split the polygon.
		 * \param _pui32LeftSides If not NULL, holds the returned number of sides in the left returned polygon.
		 * \param _ppLeftRet If not NULL, holds the returned left polygon.
		 * \param _pui32RightSides If not NULL, holds the returned number of sides in the right returned polygon.
		 * \param _ppRightRet If not NULL, holds the returned right polygon.
		 * \param _fThickness Thickness of planes.
		 */
		template <typename _tType, typename _tVecType, typename _tPolyType, typename _tPlaneType>
		static LSVOID LSE_CALL			CPhysUtils::Split( const _tPolyType &_pPoly, const _tPlaneType &_pPlane,
			LSUINT32 * _pui32LeftSides, _tPolyType * _ppLeftRet,
			LSUINT32 * _pui32RightSides, _tPolyType * _ppRightRet,
			_tType _fThickness = static_cast<_tType>(LSM_PLANE_THICKNESS) ) {
			// No way to split a polygon with fewer than 3 vertices.
			assert( _pPoly.TotalSegments() >= 3UL );

			LSUINT32 ui32FrontCount = 0UL;
			LSUINT32 ui32BackCount = 0UL;

			_tVecType vA = _pPoly[_pPoly.TotalSegments()-1]->p;
			LSM_PLANE_INTERSECT piSide = CClassify::Point<_tType, _tVecType, _tPlaneType>( vA, _pPlane, _fThickness );
			LSUINT32 ui32Total = _pPoly.TotalSegments();

			_tVecType vSplitPoint;
#define LSP_PUSHFRONT( VEC )	if ( _ppLeftRet ) { (*_ppLeftRet).Segments()[ui32FrontCount].p = VEC; } ++ui32FrontCount
#define LSP_PUSHBACK( VEC )	if ( _ppRightRet ) { (*_ppRightRet).Segments()[ui32BackCount].p = VEC; } ++ui32BackCount

			// Run over all edges of the polygon.
			for ( LSUINT32 N = 0; N < ui32Total; ++N ) {
				_tVecType vB = _pPoly[N]->p;
				LSM_PLANE_INTERSECT piSide2 = CClassify::Point<_tType>( vB, _pPlane, _fThickness );
				switch ( piSide2 ) {
					case LSM_PI_FRONT : {
						if ( piSide == LSM_PI_BACK ) {
							// Edge (A, B) crosses plane.
							CIntersect::LineSegPlaneFast<_tType, _tVecType, _tPlaneType>( vB, vA, _pPlane, vSplitPoint );
							LSP_PUSHFRONT( vSplitPoint );

							LSP_PUSHBACK( vSplitPoint );
						}
						// Always put B on the front side.
						LSP_PUSHFRONT( vB );
						break;
					}
					case LSM_PI_BACK : {
						if ( piSide == LSM_PI_FRONT ) {
							// Edge (A, B) crosses plane.
							CIntersect::LineSegPlaneFast<_tType, _tVecType, _tPlaneType>( vA, vB, _pPlane, vSplitPoint );
							LSP_PUSHFRONT( vSplitPoint );

							LSP_PUSHBACK( vSplitPoint );
						}
						else if ( piSide == LSM_PI_COPLANAR ) {
							// Output A when edge goes from on to behind the plane.
							LSP_PUSHBACK( vA );
						}
						// Always put B on the back side.
						LSP_PUSHBACK( vB );
						break;
					}
					default : {
						// B is on the plane.  Always pass it to the front side.
						LSP_PUSHFRONT( vB );
						// If A is behind the plane, also put B on the back side.
						if ( piSide == LSM_PI_BACK ) {
							LSP_PUSHBACK( vB );
						}
					}
				}

				// Next edge will be from B to the next.
				vA = vB;
				piSide = piSide2;
			}
#undef LSP_PUSHBACK
#undef LSP_PUSHFRONT

			if ( _pui32LeftSides ) { (*_pui32LeftSides) = ui32FrontCount; }
			if ( _pui32RightSides ) { (*_pui32RightSides) = ui32BackCount; }
			if ( _ppLeftRet ) {
				for ( LSUINT32 I = ui32FrontCount; I--; ) {
					(*_ppLeftRet)[I]->q = (*_ppLeftRet)[(I+1)%ui32FrontCount]->p;
				}
				(*_ppLeftRet).Plane() = _pPoly.Plane();
				(*_ppLeftRet).SetUser( _pPoly.GetUser() );
			}
			if ( _ppRightRet ) {
				for ( LSUINT32 I = ui32BackCount; I--; ) {
					(*_ppRightRet)[I]->q = (*_ppRightRet)[(I+1)%ui32BackCount]->p;
				}
				(*_ppRightRet).Plane() = _pPoly.Plane();
				(*_ppRightRet).SetUser( _pPoly.GetUser() );
			}
		}

This routine is meant to be called twice—once to check how many sides on each new polygon and once to fill them in.  As a result I used a macro to help me “push” points into each polygon, which does the NULL pointer check for me.  If you are not using stack allocators, you do not need to go through such lengths to add segments to polygons, but the advantages in speed and memory consumption generally outweigh the alternative, especially if you expect your .MAP loader to ever load next-generation map files (note that while .MAP files are deprecated, .VMF files are still being updated for current and next-generation use, and these routines work equally well for those files).

The final point worth re-mentioning is that I used an explicit stack during the BSP tree creation.  This improves the stability of the overall program, since I expect next-generation levels to have very many solids.   Recursive routines provide a chance of stack overflow, but it takes a very very complex map file to ever make that happen, so if you are following along and understand recursion better than explicit stacking then you may feel free to use recursion instead if that is more comfortable to you.  I have a machine-generated .MAP file of Area 51 from Perfect Dark which is the largest map of any GoldenEye 007 or Perfect Dark game and contains over 33,000 solids.  This still is hardly enough to cause a stack overflow here, so don’t feel too bad if you want to make your routine recursive rather than explicit.

An Apple a Day…

Now would be a good time to verify your results.  Again, just export the number of triangles and then each triangle.  The only difference is that you will be counting triangles and outputting them recursively.  These are just debug routines, but here are mine:

	/**
	 * Counts the number of triangles in a BSP node recursively.
	 *
	 * \param _pnNode The node to traverse, counting triangles along the way.
	 * \return Returns the number of triangles all the way down the node tree.
	 */
	LSUINT32 LSE_CALL CSolidLeafBspHigh::CountTris( const LSP_NODE * _pnNode ) {
		LSUINT32 ui32Total = 0UL;
		for ( LSUINT32 I = _pnNode->vPolies.Length(); I--; ) {
			ui32Total += _pnNode->vPolies[I].TotalSegments() - 2UL;
		}
		if ( _pnNode->pnFront ) {
			ui32Total += CountTris( _pnNode->pnFront );
		}
		if ( _pnNode->pnBack ) {
			ui32Total += CountTris( _pnNode->pnBack );
		}
		return ui32Total;
	}

	/**
	 * Writes the triangles to a file stream, primarily for debugging.
	 *
	 * \param _pnNode The node to traverse, outputting vertices along the way.
	 * \param _fsStream The stream out to which to write the vertices.
	 */
	LSVOID LSE_CALL CSolidLeafBspHigh::OutputVertices( const LSP_NODE * _pnNode, CFileStream &_fsStream ) {
		for ( LSUINT32 I = 0UL; I < _pnNode->vPolies.Length(); ++I ) {
			LSUINT32 ui32Total = _pnNode->vPolies[I].TotalSegments() - 1UL;
			for ( LSUINT32 J = 1UL; J < ui32Total; ++J ) {
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Segments()[0].p.x) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Segments()[0].p.y) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Segments()[0].p.z) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Plane().n.x) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Plane().n.y) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Plane().n.z) );

				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Segments()[J].p.x) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Segments()[J].p.y) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Segments()[J].p.z) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Plane().n.x) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Plane().n.y) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Plane().n.z) );

				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Segments()[J+1].p.x) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Segments()[J+1].p.y) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Segments()[J+1].p.z) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Plane().n.x) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Plane().n.y) );
				_fsStream.WriteFloat( static_cast<LSFLOAT>(_pnNode->vPolies[I].Plane().n.z) );
			}
		}

		if ( _pnNode->pnFront ) {
			OutputVertices( _pnNode->pnFront, _fsStream );
		}
		if ( _pnNode->pnBack ) {
			OutputVertices( _pnNode->pnBack, _fsStream );
		}
	}

This is basically the same routine as before, but since I reversed the normals for the solids I no longer have to export the negative normals here.  Note that I also changed the winding order by exporting J before J+1.

The Last Step

When this routine has run its course, it will generate enough planes to handle all of the polygons in the entire map.  But this is neither the most efficient routine nor the one that will help us create portals and later PVS’s.  What we need for leafs of the BSP is not just a bunch of polygons on a single plane but a convex hull of polygons that represents a room or at least a partial room.

The change we need to make is actually quite simple: For each front set of polygons, if that set of polygons forms a convex area (remember that I made all of the solids point their normals outwards from their interiors, which in turn means that a group of faces all pointing inwards is a convex area) then add it to the current node instead of the “front” node where it was originally destined.

The routine for classifying a set of polygons as convex follows.  The routine compares all other polygons against each other polygon and if any have points that test as being behind a given polygon, then the whole set of polygons is concave, not convex.  Imagine a square room.  Are any of the 4 walls behind any of the other 3 walls?

		/**
		 * Determines if the polygons in the given array form a convex region of space.
		 *
		 * \param _vPlanePolies The array of polygons on the splitting plane.
		 * \param _vPolies The array of polygons to check for forming a convex region of space.
		 * \param _fThickness Plane thickness.
		 * \return Returns true if the polygons form a convex region of space.
		 */
		LSBOOL LSE_CALL						AllAreConvex( const CVector<_tPolyType, LSUINT32, 4096UL> &_vPlanePolies, const CVector<_tPolyType, LSUINT32, 4096UL> &_vPolies, _tType _fThickness = static_cast<_tType>(LSM_PLANE_THICKNESS) ) {
			for ( LSUINT32 I = 0UL; I < _vPolies.Length(); ++I ) {
				// If any other polygons are behind this one's plane, it is not convex.
				// Check here first since it is more likely to exit early.
				for ( LSUINT32 J = I + 1UL; J < _vPolies.Length(); ++J ) {
					if ( CClassify::Polygon( _vPolies[J], _vPolies[I].Plane(), _fThickness ) == LSM_PI_BACK ) { return false; }
				}
				// Check against the plane polygons too.
				for ( LSUINT32 J = _vPlanePolies.Length(); J--; ) {
					if ( CClassify::Polygon( _vPlanePolies[J], _vPolies[I].Plane(), _fThickness ) == LSM_PI_BACK ) { return false; }
				}
			}
			return true;
		}

With this helper function in-place, it is easy to upgrade our BSP function to generate convex leaves instead of coplanar leaves.

							break;
						}
					}
				}
				if ( vFrontPolies.Length() && AllAreConvex( sThis.pnNode->vPolies, vFrontPolies, _fThickness ) ) {	// Start new code.
					// Add them to the front node.
					if ( !sThis.pnNode->vPolies.Append( &vFrontPolies[0], vFrontPolies.Length() ) ) {
						return false;
					}
					vFrontPolies.ResetNoDealloc();
				}													// End new code.

				sThis.pnNode->vPolies.Snap();
				if ( vFrontPolies.Length() ) {

Anything you add to the current node instead of children nodes is something that does not need to be split etc.  Less time is spent checking for splitting nodes and fewer triangles are generated in the final result, so this helps to reduce the number of final triangles and conversion time heavily, but that is just a bonus on top of its real goal, which is to create convex spaces in which to generate portals and later PVS’s.

Check Your Results

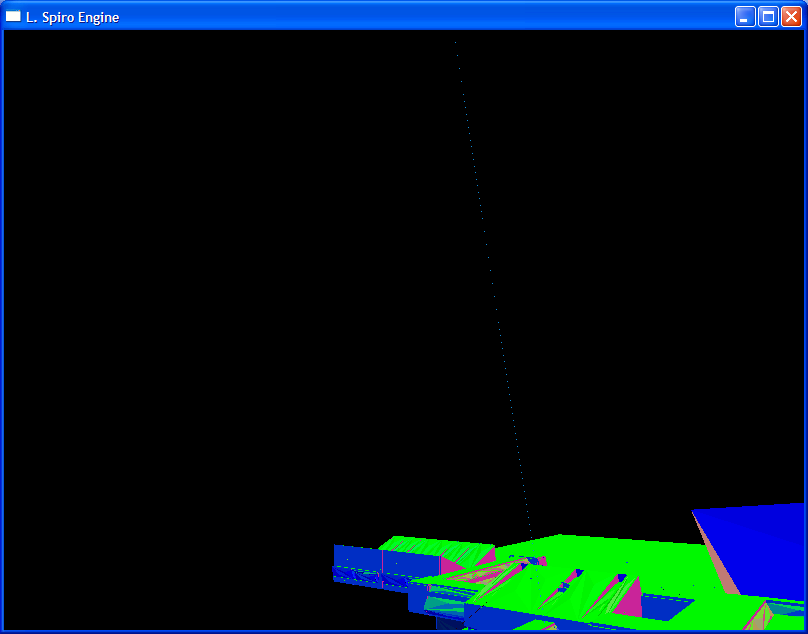
After implementing all of this it would be a good idea to check your results.  The same routine for gathering BSP polygons I provided above will be able to check all of your conversions for stability now too.  If your BSP epsilon is too low you might see artifacts such as these:

Where is that blue line going?  The epsilon you pass to the BSP tree is the most important, and should be handled with care.  So far I have been passing 0.00000000001 with good results, but all my math is done in double-floating-point precision.  If you insist on using 32-bit floating-point epsilons, I am not sure what value to pass, but keep passing increasing values until these kinds of artifacts go away.  While working with 64-bit doubles, the value I am passing is (2.2204460492503131e-016*1000.0).

In Conclusion

If you have followed along carefully you will be able to make your own displays of .MAP files and have a little bit of information on rooms and such.  Part of this is just the nature of working with solids, but part of this will be exposed in upcoming tutorials, where we will get into collision detection and portal culling.

My goal here was to leave you off with a set of data that is as good as rendering the first set of data, but with data regarding interiors etc.

L. Spiro