Overview
This tutorial will present an efficient implementation of quadtrees. It is expected that you have at least a basic understanding of what quadtrees are and do, and if not you can read about them here: http://en.wikipedia.org/wiki/Quadtree
Although they improve performance in algorithms related to searching for visible objects or in detecting collisions for physics, quadtrees and octrees have a reputation for lacking in efficiency in certain areas, particularly related to the cache and also insertion speeds. As objects move within a quadtree they sometimes have to be inserted into different cells, and typical implementations do this by searching from the root cell down. In regards to the cache, typical implementations will allocate cells separately for each parent cell (that is, each parent has 4 child cells, so 4 cells are allocated together for each parent), which means cells may end up in completely different areas of RAM which is bad for the cache. Here, I will explain how to handle both of these issues and provide an implementation for a quadtree with good caching and constant, and almost instant, insertion time.
Basic Framework
We start with a the basic quadtree classes you would find in any quadtree implementation:
class CQuadTreeNode;
/**
* Class CQuadTreeObject
* \brief An object that can be fit into a quad-tree must inherit from this.
*
* Description: An object that can be fit into a quad-tree must inherit from this.
*/
class CQuadTreeObject {
public :
// == Various constructors.
LSE_CALLCTOR CQuadTreeObject();
LSE_CALLCTOR ~CQuadTreeObject();
// == Functions.
/**
* Sets the quad-tree node into which this object has been inserted.
*
* \param _pqtnNode The node into which this object has been inserted.
*/
LSVOID LSE_CALL SetQuadTreeNode( CQuadTreeNode * _pqtnNode );
/**
* Must be overloaded to return a constant reference to a 2D AABB.
*
* \return Returns a constant reference to a 2D AABB.
*/
virtual const CAabb2d & LSE_CALL QuadTreeAabb() const = 0;
/**
* Gets the quad-tree node into which this object is inserted.
*
* \return Returns the quad-tree node into which this object is inserted, if any.
*/
LSE_INLINE const CQuadTreeNode * LSE_CALL QuadTreeNode() const;
protected :
// == Members.
/**
* The node to which this object has been added.
*/
CQuadTreeNode * m_pqtnNode;
};
This is a base class from which anything that wants to be an object inside the quadtree needs to inherit. It is meant to be a child class for your sprites and other 2D scene elements. It doesn’t have any functionality except to set and get the quadtree node to which this object belongs (which are so simple that no code is necessary to show these), and a pure virtual to make sure there is a 2D axis-aligned bounding box for the quadtree to use to decide where to put this object.
Next, a quadtree is composed of nodes.
/**
* Class CQuadTreeNode
* \brief A node in a quad-tree.
*
* Description: A node in a quad-tree.
*/
class CQuadTreeNode {
friend class CQuadTree;
public :
// == Various constructors.
LSE_CALLCTOR CQuadTreeNode();
LSE_CALLCTOR ~CQuadTreeNode();
// == Functions.
/**
* Sets the center and radius of the node.
*
* \param _vPos Center of the node.
* \param _fRadius Radius of the node.
*/
LSVOID LSE_CALL SetCenterAndRadius( const CVector2 &_vPos, LSREAL _fRadius );
/**
* Gets the center of the node.
*
* \return Returns the center of the node.
*/
LSE_INLINE const CVector2 & LSE_CALL GetCenter() const;
/**
* Gets the radius of the node.
*
* \return Returns the radius of the node.
*/
LSE_INLINE LSREAL LSE_CALL GetRadius() const;
/**
* Sets a child.
*
* \param _ui32Index Index of the child to set.
* \param _pqtnChild Pointer to the child node.
*/
LSVOID LSE_CALL SetChild( LSUINT32 _ui32Index, CQuadTreeNode * _pqtnChild );
/**
* Adds an object to the node.
*
* \param _pqtoObject The object to add to the node.
* \return Returns true if there were no memory allocation issues.
*/
LSBOOL LSE_CALL AddObject( CQuadTreeObject * _pqtoObject );
/**
* Removes an object from the node.
*
* \param _pqtoObject The object to remove from the node.
*/
LSVOID LSE_CALL RemObject( CQuadTreeObject * _pqtoObject );
protected :
// == Members.
/**
* Linked list of objects in this node.
*/
CSingleLinkedList<CQuadTreeObject *> m_sllObjects;
/**
* The 4 children of this node.
*/
CQuadTreeNode * m_pqtnChildren[4];
/**
* The center of the node.
*/
CVector2 m_vCenter;
/**
* The radius of the node.
*/
LSREAL m_fRadius;
};
Once again everything is self-explanatory. Each node has a center point and 4 children pointers. Since nodes are always perfectly square we can simplify its representation by holding just a radius instead of an X and Y half-distance. It also has a list of all the objects that are inside of its box. A linked list is used for better insertion and deletion times, though there are merits to using a vector for better caching. In order to get this merit in linked lists, however, you can precache the next node as you traverse the list. Vectors also require fewer allocations and are more memory-conservative, so you are very welcome to experiment and see which is better for you. In fact you may want to make a macro to toggle between vectors and linked lists on a per-game basis since it may change depending on your game. I will only show how to use linked lists here.
I won’t show the implementation for this class either because it is so basic, but it is important to note that this class does not allocate directly. It stores pointers to its children, but it does not allocate them—they have already been allocated in a pool. That is because of how we handle caching.
Caching
Caching is actually the easiest problem to tackle—instead of allocating cells separately, a single large bucket of cells is allocated. Not only does this provide better caching, it is faster to create and destroy (a single allocation is made instead of 1,365 allocations), and it consumes less overall memory, as there would otherwise be extra allocated data for each of those 1,365 allocations (for example, if you allocate 1 byte, the system often internally allocates 20 bytes total, possibly more).
Our tree will have 8 levels total, and later we will discover that these levels correlate to the 8 bits in a byte. But first, knowing that we will have 8 levels, we can calculate the number of nodes we need as follows:
/** * The number of nodes in this tree. */ #define LSP_QUAD_NODES (1UL+2UL*2UL+4UL*4UL+8UL*8UL+16UL*16UL+32UL*32UL+64UL*64UL+128UL*128UL)
We are including the root node for better caching.
The Quadtree Structure
Now we have the 2 helper classes in place and we have considered how to cache the nodes by putting them into a pool. We also know how many knows there will be in that pool. Now we can begin actually making the quadtree class.
/**
* Class CQuadTree
* \brief An 8-layer quad-tree with fast insertion times.
*
* Description: An 8-layer quad-tree with fast insertion times. Uses a bit hack to increase insertion speed
* for high-performance use.
*/
class CQuadTree {
public :
// == Various constructors.
LSE_CALLCTOR CQuadTree();
LSE_CALLCTOR ~CQuadTree();
// == Functions.
/**
* Creates the quad-tree with the given size. The created quad-tree has 8 nested layers.
*
* \param _fSize The size of the quad-tree to create.
* \return Returns true if there were no memory failures during the creation of the quad-tree.
*/
LSBOOL LSE_CALL CreateQuadTree( LSREAL _fSize );
/**
* Resets the quad-tree back to nothing.
*/
LSVOID LSE_CALL Reset();
/**
* Gets the root node of the tree, which can be NULL.
*
* \return Returns the root node of the tree, which can be NULL.
*/
const CQuadTreeNode * LSE_CALL Root() const;
protected :
// == Members.
/**
* Pointer to the nodes of the quad-tree. The first node encompasses the
* entire bounding box of this tree.
*/
LSUINT8 * m_pui8Nodes;
/**
* Pointers to each level of the tree, with index 0 being the root node.
*/
CQuadTreeNode * m_pqtnLevels[8];
/**
* The radius of this quad-tree.
*/
LSREAL m_fRadius;
/**
* The inverse radius of the quad-tree.
*/
LSREAL m_fInvRadius;
// == Functions.
/**
* Gets the root node of the tree, which can be NULL.
*
* \return Returns the root node of the tree, which can be NULL.
*/
LSE_INLINE CQuadTreeNode * LSE_CALL Root();
};
Most of this explains itself, but it should be noted that we store not an array of nodes but an array of unsigned 8-bit integers that act as the pool node. This decision is something of personal preference because it helps me in a technical way to think about the pool of nodes as just that: a pool. In a way, it says to me that this array of nodes is not meant to be used like an array—for example it can’t be indexed or iterated. However you are free to store your pool of nodes as just an array of nodes.
There are only 2 functions of real interest here, but I will start with the smaller clean-up functions first.
The constructor and destructor:
// == Various constructors.
LSE_CALLCTOR CQuadTree::CQuadTree() :
m_pui8Nodes( NULL ) {
}
LSE_CALLCTOR CQuadTree::~CQuadTree() {
Reset();
}
The helper Reset():
/**
* Resets the quad-tree back to nothing.
*/
LSVOID LSE_CALL CQuadTree::Reset() {
if ( m_pui8Nodes ) {
CQuadTreeNode * pqtnNodes = Root();
// The number of nodes is fixed.
for ( LSUINT32 I = LSP_QUAD_NODES; I--; ) {
pqtnNodes[I].~CQuadTreeNode();
}
LSEDELETE [] m_pui8Nodes;
m_pui8Nodes = NULL;
}
}
Note again you would have to just delete [] the array if you used a pool that is of the CQuadTreeNode type directly.
Instant-Insertion
We have discussed caching but not yet instant-insertion. We will employ a bit hack that was presented in Game Programming Gems II by Matt Pritchard.
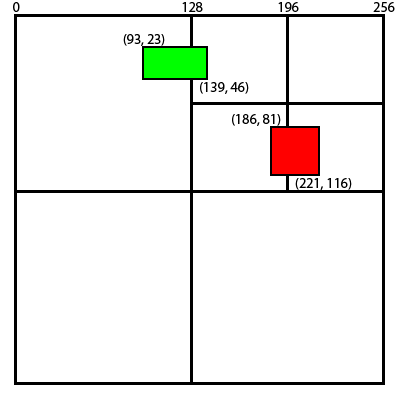
Examine the 2 objects in the image below.
By looking it is easy to see that the green box belongs in the root node and the red box belongs one level down, but how can we determine this instantly?
When the world coordinates range from 0 to 256, we can use the properties of a byte and some bit tricks to figure out the level of each object instantly. We examine the spans of each object along each axis (X and Y) and use logical XOR to produce a bit pattern. First, for the green box, its X extends are 93 (01011101) and 139 (10001011). 93 XOR 139 = 214 (11010110). The highest bit set is at index 7. Subtract the maximum bit index (there are 8 levels in the tree so the highest index is 7) and the result is 0, which is indeed the root node.
Let’s keep looking at the green block for the next example. Imagine that it’s left side was nudged over the 128 axis a bit, so now its X extents are 130 and 139. Only the left side was nudged.
130 (10000010) XOR 139 (10001011) = 9 (00001001). The highest-set bit in 00001001 is at index 3. 7 – 3 = 4. If we had 4 levels, it would be 4 levels deep.
Moving on to the red object, 168 (10101000) XOR 221 (11011101) = 117 (01110101). Highest bit is the 6th. 7 – 6 = 1. Along the X, it is easy to visually confirm that the red object is 1 level deep.
So far we have looked only at the X. Ultimately, you have to look at both axes and take the larger of the 2. Our modified green object was found to be at level 4 by the X axis, but the result of its Y axis is: 23 (00010111) XOR 49 (00101110) = 57 (00111001). 7 – 5 = 2. The the larger level (closer to the root) between levels 4 and 2 is 2. The modified green object would be in level 2.
Finding the Exact Node
We can find the level easily, so how do we find the actual node in that level? If we lay out the nodes in RAM properly it is very easy to index into them once we find the starting point of the given level. That means we will be laying them out in RAM in a grid-like fashion.
Implementing It
Now for the first interesting function: CreateQuadTree(). It begins by creating the pool.
/**
* Creates the quad-tree with the given size. The created quad-tree has 8 nested layers.
*
* \param _fSize The size of the quad-tree to create.
* \return Returns true if there were no memory failures during the creation of the quad-tree.
*/
LSBOOL LSE_CALL CQuadTree::CreateQuadTree( LSREAL _fSize ) {
Reset();
// The number of nodes is fixed.
// We are "hacking" the array of nodes in order to save space. Rather than allocating
// each node, which incurs a lot of wasted memory, we are storing them sequentially
// in a single buffer.
m_pui8Nodes = LSENEW LSUINT8[LSP_QUAD_NODES*sizeof( CQuadTreeNode )];
if ( !m_pui8Nodes ) { return false; }
CQuadTreeNode * pqtnNodes = Root();
for ( LSUINT32 I = LSP_QUAD_NODES; I--; ) {
new( &pqtnNodes[I] ) CQuadTreeNode();
}
m_fInvRadius = static_cast<LSREAL>(255.0) / _fSize;
It keeps the inverse size of the tree so that it can quickly (using a single multiplication) convert objects from world space to 0.0 – 255.0 space for our bit hacks to work. All of the nodes have been constructed but they haven’t been attached to each other in a tree-like fashion, nor have their bounds been set. This is the most complex part of the whole process.
// Nodes are stored so that all nodes in a level are sequential in memory until
// the next level. Within each level, the nodes are 2D arrays of equal width
// and height, double the previous layer. There are 8 layers, with the first
// being 1-by-1 and the last being 128-by-128.
//
// This loop goes over each level
CQuadTreeNode * pqtnThis = pqtnNodes, * pqtnLast = NULL;
LSREAL fFull = _fSize;
_fSize *= LSM_HALF;
m_fRadius = _fSize;
CVector2 vOffset( -_fSize, -_fSize );
for ( LSUINT32 I = 0UL; I < 8UL; ++I ) {
m_pqtnLevels[I] = pqtnThis;
// For each node at this level.
for ( LSUINT32 Y = (1UL << I); Y--; ) {
CQuadTreeNode * pqtnRow = &pqtnThis[Y*(1UL<<I)];
LSREAL fYPos = LSREAL( Y ) / LSREAL( 1UL << I ) * fFull + _fSize;
for ( LSUINT32 X = (1UL << I); X--; ) {
pqtnRow[X].SetCenterAndRadius( CVector2( LSREAL( X ) / LSREAL( 1UL << I ) * fFull + _fSize, fYPos ) + vOffset,
_fSize );
if ( pqtnLast ) {
// There is a parent. Get its index.
LSUINT32 ui32ParentX = X >> 1UL;
LSUINT32 ui32ParentY = Y >> 1UL;
LSUINT32 ui32ParentIndex = (ui32ParentY * (1UL << (I - 1UL))) + ui32ParentX;
LSUINT32 ui32X = X & 1UL;
LSUINT32 ui32Y = Y & 1UL;
pqtnLast[ui32ParentIndex].SetChild( (ui32Y << 1UL) + ui32X, &pqtnRow[X] );
}
}
}
pqtnLast = pqtnThis;
pqtnThis += (1UL << I) * (1UL << I);
_fSize *= LSM_HALF;
}
return true;
}
The first for() loop goes over each level. Then along the Y axis and for each Y axis all of the X’s are handled. (1UL << I) is the total number of nodes for each axis, so level 0 has 1 node, level 1 has 2, 2 has 4, etc. The best way to understand it is to simply stare at it until you do.
For each node, after its position and radius are set, it checks to see if it has a parent (as in not level 0) and if so it reverses the grid to find out where its parent is and determines which of its 4 children this node is. m_pqtnLevels keeps an array to the first node in each level for use later.
The next interesting function is the one for inserting objects into nodes. We will make use of everything we know so far to ensure it has blazing speed.
/**
* Inserts an object into the quad-tree. Any items not fully inside the bounds of the quad-tree
* are inserted at the root level. The insertion process is extremely efficient.
*
* \param _pqtoObject The quad-tree-object to insert.
* \return Returns true if there are no memory failures during the insert.
*/
LSBOOL LSE_CALL CQuadTree::InsertObject( CQuadTreeObject * _pqtoObject ) {
const CAabb2d & a2Box = _pqtoObject->QuadTreeAabb();
if ( a2Box.m_vMin.x < -m_fRadius || a2Box.m_vMax.x > m_fRadius ||
a2Box.m_vMin.y < -m_fRadius || a2Box.m_vMax.y > m_fRadius ) {
return Root()->AddObject( _pqtoObject );
}
Firstly a bounds check. If it is partially or fully outside of the area contained by the quadtree, add it to the root and leave.
Next we perform a few very quick conversions, specifically converting from world coordinates to the 0-255 range we need for our bit hacks.
// The quad-tree exists in the range from -m_fRadius to m_fRadius. // Convert to the range 0 to (m_fRadius * 2). CAabb2d a2Shifted; a2Shifted.m_vMin = a2Box.m_vMin + CVector2( m_fRadius, m_fRadius ); a2Shifted.m_vMax = a2Box.m_vMax + CVector2( m_fRadius, m_fRadius ); // Now to the range from [0..255]. a2Shifted.m_vMin.x *= m_fInvRadius; a2Shifted.m_vMin.y *= m_fInvRadius; a2Shifted.m_vMax.x *= m_fInvRadius; a2Shifted.m_vMax.y *= m_fInvRadius; // Convert to integers and clamp. LSUINT32 ui32MinX = static_cast<LSUINT32>(CStd::Clamp( CMathLib::Floor( a2Shifted.m_vMin.x ), LSM_ZERO, static_cast<LSREAL>(255.0) )); LSUINT32 ui32MaxX = static_cast<LSUINT32>(CStd::Clamp( CMathLib::Ceil( a2Shifted.m_vMax.x ), LSM_ZERO, static_cast<LSREAL>(255.0) )); LSUINT32 ui32MinY = static_cast<LSUINT32>(CStd::Clamp( CMathLib::Floor( a2Shifted.m_vMin.y ), LSM_ZERO, static_cast<LSREAL>(255.0) )); LSUINT32 ui32MaxY = static_cast<LSUINT32>(CStd::Clamp( CMathLib::Ceil( a2Shifted.m_vMax.y ), LSM_ZERO, static_cast<LSREAL>(255.0) ));
Now we are ready to get the level using our bit hacks.
// Get the level at which the object will be inserted.
LSUINT32 ui32X = ui32MinX ^ ui32MaxX;
if ( !ui32X ) { ui32X = 7UL; } // 100% flat objects go to the highest (smallest) level.
else { ui32X = 7UL - CStd::HighestBit( ui32X ); }
LSUINT32 ui32Y = ui32MinY ^ ui32MaxY;
if ( !ui32Y ) { ui32Y = 7UL; } // 100% flat objects go to the highest (smallest) level.
else { ui32Y = 7UL - CStd::HighestBit( ui32Y ); }
LSUINT32 ui32Level = CStd::Min( ui32X, ui32Y );
Notice that we handle the edge cases of fully flat objects by putting them into level 7, which is the smallest size for nodes. Next we take advantage of our grid-like structure, calculate the X and Y indices of the node that owns this object, and add it to the node.
// Now we know which level in the tree it is. // Find out which node on that level owns it. ui32X = ui32MinX >> (8UL - ui32Level); ui32Y = ui32MinY >> (8UL - ui32Level); // Add it to the node. #ifdef _DEBUG CQuadTreeNode * pqtnNode = &m_pqtnLevels[ui32Level][ui32Y*(1UL<<ui32Level)+ui32X]; assert( pqtnNode->GetCenter().x - pqtnNode->GetRadius() <= a2Box.m_vMin.x ); assert( pqtnNode->GetCenter().x + pqtnNode->GetRadius() >= a2Box.m_vMax.x ); assert( pqtnNode->GetCenter().y - pqtnNode->GetRadius() <= a2Box.m_vMin.y ); assert( pqtnNode->GetCenter().y + pqtnNode->GetRadius() >= a2Box.m_vMax.y ); #endif // #ifdef _DEBUG return m_pqtnLevels[ui32Level][ui32Y*(1UL<<ui32Level)+ui32X].AddObject( _pqtoObject ); }
With some debug code we can verify that we have put the 2D object into the correct location.
Conclusion
The downsides of quadtrees is that they are often implemented in such a way that they have poor caching and slow insertion times. I have provided an implementation that provides nearly instant insertion times no matter how deep objects are within the tree and heavily improves caching by eliminating the recursive node search typically associated with insertion and by keeping all the nodes local to each other in one giant pool of memory.
An instant-insert octree could be built off these same principals. Since it is not feasible to have 8 levels in an octree due to memory constraints, one method would be to use this approach as-is, updgraded to 3D, and with a limit on the depth, such as 3 or 4. Another approach could be to use this method as-is for just the Z and X axes and use a grid for the Y (vertical) axis. Most games have fairly flat worlds, so this is a good method overall.
L. Spiro

Hello L. Spiro,
Please forgive my assumption here on your excellent article, but does insertion = removal? Are the removing of objects just as efficient as inserting them?
I hope all is well with you.
Thanks!
SC
Removal is always trivial because the object stores a pointer to the node in which it resides and that pointer can be used to immediately remove itself from that node.
Only insertion is typically slow because it normally involves a search from the root node down until you find the smallest node that can contain the object. Implicitly, this also means that objects 8 levels deep are extremely slow to insert with typical implementations.
Here, there is no search, so insertion is always fast regardless of how deep into the tree the object is.
L. Spiro
Awesome article! Enjoyed reading it. =)
I think I did find a typo however, that kinda threw me off until reading on further and then backtracking a bit.
The line:
“Subject the maximum bit index (there are 8 levels in the tree so the highest index is 7)…”
should be:
“Subtract the maximum bit index (there are 8 levels in the tree so the highest index is 7)…”
At least I think.. =)
Please correct me if I’m wrong.
Gerald
Nice find; I have fixed it, thank you.
L. Spiro
neat
Thanks for the helpful article on fast Quad-Trees.
So if I understand correctly, is it better to instantiate all the sub-nodes ahead of time in memory (aka: when the game starts) before you begin inserting objects in the QuadTree during the game-loop?
It sounds like that could create quite a massive amount of nodes if you had a large 2d side-scrolling platformer (depending on how many levels deep your QuadTree is set to, I suppose).
You’ve also mentioned 8-levels deep in your example, is this a norm? Could a QuadTree in theory use up all bits in an Unsigned Integer (though that would probably be WAY too many levels and defeat the purpose of using the QuadTree!) So although not realistic… is this possible?
Also, I see that you split up your arrays/lists (sorry for wrong terminology, I’m from an ActionScript background) by levels, which makes sense. But would it optimize the QuadTree even further if you brought all the nodes into one big massive list? Knowing the first 4 are at Level 1, the next 16 at Level 2, the next 64 at Level 3… etc, could that be another way to store the nodes?
You would create all the nodes in the quadtree up-front in either case as soon as the user specifies the size of the world (or the world is loaded from a file etc.).
8 levels is usually the maximum. More than that and you start to pay a huge price in memory and the nodes become so small that objects change nodes more frequently as they move through them. More nodes does not always equal better performance; 8 is just about the right trade-off between memory and performance, though yes you could theoretically take it more nodes deep with some modifications.
I am not sure about your last question. What you are describing about the nodes being tightly packed such that the first 4 are together, followed by the next 16, following by the next 64, is what this quadtree does. All of the nodes are in a single pool in order of level.
L. Spiro
Oh damn, I only noticed your reply after I’ve posted an example on my blog, haha!
I want to thank you very much again for this article. I’m not familiar with C++ (correct me if I’m wrong in assuming that’s what your example is using), but after reading it over and over a few times, I got it working like this :
Flash Demo (SWF):
http://pierrechamberlain.ca/demo.php?demo=Pierre_FastTree_test&folder=others
I’m not sure I’ve fully implemented it optimally like yours does, but hey, the memory isn’t climbing up the stratosphere, so I’m a happy camper!
So far I’ve built a few methods to:
- get all the parents of a given Node;
- get all children under a given Node;
- get all the “deepest” children under a Rectangle area;
- get all related nodes (children and parents) under a Rectangle area;
What you see being applied to the Block that follows the mouse is the ‘findAllRelatedNodes()’ method.
Anyways, just wanted to share the news! I’ll likely be implementing more to it later on.
Hi L. Spiro,
Great article, I read it when you first posted it but have since decided to try and implement it in flash just out of curiosity.
Very quickly I tested the insertion method and it was indeed very quick, 10,000 inserts in about 1ms pre optimisation – v quick indeed.
A quick note on speeding it up just a touch though, you make 2 calls to CStd::HighestBit, where I am pretty sure you can OR the values beforehand and save the call. In C I doubt it will save you much but in AS3 it is faster to replace a function call with a single bitwise operation by quite a margin.
Something like:
LSUINT32 ui32XY = (ui32MinX ^ ui32MaxX) | (ui32MinY ^ ui32MaxY);
Anyway, I thought I would ask you how you would use your implementation for 2D collision detection, it seems that by creating all the nodes upfront you would have to traverse every single one to find out if any data was in there, i.e. you cannot stop early because it has no more children. I could be completely missing the point here (I have never played with quadtrees before so I could be way off the mark). So it seems you gain great speed with the inserts but then maybe lose out when it comes to getting a potential hit list for a given object. If I am wrong (and I probably am) please do share with me what I am missing.
Another super quick note on storing the objects in the nodes, how would you recommend storing them for fastest insert/traversal/deletion, some sort of linked list?
Thanks again for a cool article, I am fan of using bitwise math to smash though the speed limits imposed by standard methods!
Thank you.
CStd::HighestBit() actually reduces to basically an inlined BSR instruction on x86, so it is pretty efficient. I don’t think there is a way to avoid handling them separately since the minimum of the 2 values is required later. If we were searching for the lowest-set bit between them or the maximum highest-set bit they could definitely be combined before any bit-searching. But there might be some bit-hacks that I haven’t considered; those are sometimes pretty tricky to find.
For this implementation I stored the objects in the nodes using a linking list, but the best way to go is most likely a hybrid between arrays and linked lists. You would basically have a linked list of 10 or so objects in each list. The array of 10 would be tightly packed so you would scan by going to a linked-list node and there would be an array of 10 objects over which you would then scan before moving on to the next linked-list node.
I haven’t tested it but it may be the best or close to the best in theory, at least.
Gathering objects for a potential collision with a specific object is done in the standard way, and is a method with too much detail to be outlined here.
But in terms of performance, the entire quad-tree is held in contiguous RAM making it very cache-friendly. Even though you don’t have early-outs when going down potentially empty nodes, going into nodes is in itself very fast.
L. Spiro
Cheers for the reply,
With regards to the HighestBit function calls, another benefit of OR first is that you no longer need the:
LSUINT32 ui32Level = CStd::Min( ui32X, ui32Y );
as the level returned is guaranteed to be the lowest one already.
If you consider your green rectangle:
var x:int = 93 ^ 139; //11010110 highest bit = 7, 7-7 = 0
var y:int = 23 ^ 46; //00111001 highest bit = 5, 7-5 = 2
var xy:int = x | y; //11111111 highest bit = 7, 7-7 = 0
As you can see the 7-(highest bit from x|y ) gives you the same as Math.min(7-(highest bit from y), 7-(highest bit from y));
So while it is a very small gain, in as3 that is a reduction of 2 functions (even if in-lined) for a simple bitwise or.
I might have missed something major here but as far as I can tell this works just fine.
So in theory your code:
// Get the level at which the object will be inserted.
LSUINT32 ui32X = ui32MinX ^ ui32MaxX;
if ( !ui32X ) { ui32X = 7UL; } // 100% flat objects go to the highest (smallest) level.
else { ui32X = 7UL – CStd::HighestBit( ui32X ); }
LSUINT32 ui32Y = ui32MinY ^ ui32MaxY;
if ( !ui32Y ) { ui32Y = 7UL; } // 100% flat objects go to the highest (smallest) level.
else { ui32Y = 7UL – CStd::HighestBit( ui32Y ); }
LSUINT32 ui32Level = CStd::Min( ui32X, ui32Y );
Could be reduced to just:
// Get the level at which the object will be inserted.
LSUINT32 ui32Level = (ui32MinX ^ ui32MaxX) | (ui32MinY ^ ui32MaxY);
if ( !ui32Level ) { ui32Level = 7UL; } // 100% flat objects go to the highest (smallest) level.
else { ui32Level = 7UL – CStd::HighestBit( ui32Level ); }
Once again I could be being a bit special here and be completely wrong so forgive me if I am.
Maybe you have benchmark app to see time messurements in ms (for about 10k objects)?
I currently don’t but I am considering it in a book I am to release this year. I have tested it on iOS as well as PC and in both cases it really improves performance, even though I don’t have any specific numbers to back the claim for now. In both (iOS and PC) cases I have populated a world with over 100,000 objects and let the tree determine the FPS. On iOS the results were very acceptable. It slowed down more than usual when many objects were grouped together and on the screen, but as soon as even 20% of the objects left the screen the result was faster than not using a quad-tree at all. And from there it climbed to 60 FPS even though every object was being advanced within the game world. Without the quad-tree, every one of the 100,000 objects was advanced, but also drawn. In the end, even if none of them were on the screen, issuing draw calls to them all never allowed the FPS to go over 20 or so. That is as much as I can give you on the metrics of time saved using this algorithm.
L. Spiro
I was wondering if you were going to write anymore articles on the engine development. It seems to have just stopped over a year ago. Should we consider it dead, or we going to need to buy the book?
The engine is not dead at all, but due to my increasing schedule on the acting side and the book, I have decided to put the engine on hold until the book is done. After that I intend to get full-swing back into the engine.
L. Spiro
So maybe you already has numbers, ms, testing environment… Would be great to compare results
I will likely post some numbers for the octree adaptation later. I can post raw results for this implementation but I won’t be making a standard quadtree for comparison, so the numbers will just be the numbers, not comparisons.
L. Spiro
oh no I mean,i want to compare results with my algorithm. Last year I was made for my game as I think not bad algorithm of broadphase collision checks, but there are nothing to compare to on the internet. So thats why it would be very great to find out is it worth something.
This isn’t Assembly….. me no want!
Nahhh good tut buddy
Your Quadtree can be used in Physics Simulation, Frustum Culling and other stuff like Ray-Casting?
About the Sweep And Prune Technique, do you think is better than that?
It can be. I already use it for frustum culling on iOS and it is very fast even with 3,000 objects.
It should be similar to prune and sweep.
L. Spiro
Hi,
thank you for this awesome article.
It really helped me to understand quadtrees better.
One thing I don’t get is the XOR-trick you use to determine the level for the rect.
I do understand that this is a working algorithm, but why does it work this way and not differently?
I’ve only used XORs to manipulate bits and never for “mathematical” applications.
Perhaps, do you have any link for me that explains the mathematical rules for Bit-operations?
Hello,
Your article seems very interesting, although I’m quite new to c++ and I don’t really understand your way of coding.
For example what is all these LS things? LSVOID, LSE_CALL, LSE_CALLCTOR, etc…
In my understanding it seems to be macros (because I heard that macros are in Capital letters) used for declaring data types (bool, void, real, etc…)
Can you enlighten me a bit about that, what are those, why do you use them, so I can read along your code fluidly?
Thanks, Max.
Sorry, this comment was hidden since January.
Those are typedef’s or macros.
typedef void LSVOID;
typedef float LSREAL;
LSE_CALL could be __stdcall or __cdecl or etc.
LSE_CALLCTOR is a constructor call, which must be __cdecl.
For the most part, if it is not obvious what it means, you don’t have to worry about it too much. If there are important points that matter but which might be hard to read or confusing, I will point them out or reformat them to be easier to read.
L. Spiro
Hello.
Very interesting algorithm! I think this algirithm very similar, to grid. But grid is easy to implement, and faster (or like) this algirithm?
Grid is linear in memory, for avoid memory fragmentation.
Objects in grid cells may be also keepd in linklist.
For search grid cell – also using only 1 shift for each coordinate.
Or, I am wrong?
P.S. I want to test this with others, but worked source not found. Maybe, someone, have worked source of this nice algorithm, on any language?
This might not be the most useful comment but I just wanted to thank you. For this, and your gamedev.net posts. It’s helping tremendously. I adjusted the code to my own syntax and it’s all good, should give it all the functionality soon that my octree has and see how it fares, expecting great improvements
My current implementation is slower (it’s still acceptable) because I use it to search for steering neighbours of a lot of tower defense minions within a radius naively (no caching yet) and that’s a lot of queries per frame, it adds up.
Since lists need to be created on the fly, to get all neighbours back to each entity, do you think a pool allocator (reset per frame/query) would be a good idea for that? I’ve been thinking about one for a few other things.
I would actually mess around a bit changing the backing between std::list and std::vector, and I don’t know about resetting it every frame. How often things get inserted and removed can be different depending on how it is used, so each backing method can offer different performances depending on the game even though everything else might be the same.
If you really want to get crazy with a minion path-finding routine in a “League of Legends” type game, the GPU should give you the best performance. You could do it in compute shaders if necessary.
L. Spiro